题目内容
(本小题共14分)
已知椭圆C的左、右焦点坐标分别是![]() ,
,![]() ,离心率是
,离心率是![]() ,直线y=t椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
,直线y=t椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。
(共14分)
解:(Ⅰ)因为![]() ,且
,且![]() ,所以
,所以![]()
所以椭圆C的方程为![]()
(Ⅱ)由题意知![]()
由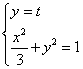 得
得![]()
所以圆P的半径为![]()
解得![]() 所以点P的坐标是(0,
所以点P的坐标是(0,![]() )
)
(Ⅲ)由(Ⅱ)知,圆P的方程![]() 。因为点
。因为点![]() 在圆P上。所以
在圆P上。所以![]()
设![]() ,则
,则![]()
当![]() ,即
,即![]() ,且
,且![]() ,
,![]() 取最大值2.
取最大值2.

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是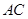 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.