题目内容
已知{an}满足: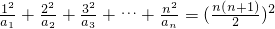 (n=1,2,3,…).
(n=1,2,3,…).
(Ⅰ) 求{an}的通项公式;
(Ⅱ) 若数列{bn}满足,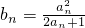 (n=1,2,3,…),试{bn}前n项的和Sn.
(n=1,2,3,…),试{bn}前n项的和Sn.
解:(Ⅰ)由 ①
①
当n≥2时,
 ②
②
①-②得: =n3,
=n3,
所以,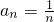 (n≥2).
(n≥2).
当n=1时,a1=1符合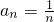 ,所以,
,所以,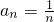 ;
;
(Ⅱ)由 =
= .
.
所以,Sn=b1+b2+…+bn
=
=
= .
.
分析:(Ⅰ)模仿题目给出的递推式,取n=n-1得到另一递推式,两式作差后即可得到结论;
(Ⅱ)把(Ⅰ)中求得到an代入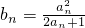 ,整理后利用裂项相消可求{bn}前n项的和Sn.
,整理后利用裂项相消可求{bn}前n项的和Sn.
点评:本题考查了数列的递推式,考查了等差数列的通项公式的求法,考查了一种重要的数列求和公式的方法,即裂项相消法,该题需要注意的是,采用列项相消时最前边和最后边剩余的项,此题是中档题.
 ①
①当n≥2时,
 ②
②①-②得:
 =n3,
=n3,所以,
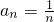 (n≥2).
(n≥2).当n=1时,a1=1符合
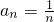 ,所以,
,所以,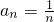 ;
;(Ⅱ)由
 =
= .
.所以,Sn=b1+b2+…+bn
=

=

=
 .
.分析:(Ⅰ)模仿题目给出的递推式,取n=n-1得到另一递推式,两式作差后即可得到结论;
(Ⅱ)把(Ⅰ)中求得到an代入
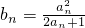 ,整理后利用裂项相消可求{bn}前n项的和Sn.
,整理后利用裂项相消可求{bn}前n项的和Sn.点评:本题考查了数列的递推式,考查了等差数列的通项公式的求法,考查了一种重要的数列求和公式的方法,即裂项相消法,该题需要注意的是,采用列项相消时最前边和最后边剩余的项,此题是中档题.

练习册系列答案
相关题目
已知{an}满足a1=a2=1,
-
=1,则a6-a5的值为( )
| an+2 |
| an+1 |
| an+1 |
| an |
| A、0 | B、18 | C、96 | D、600 |