题目内容
已知x2+y2=1,x>0,y>0,且loga(1+x)=m,loga
=n,则logay2等于( )
| 1 |
| 1-x |
| A、m+n | ||
| B、m-n | ||
C、
| ||
D、
|
考点:对数的运算性质
专题:函数的性质及应用
分析:由已知得logay2=loga(1-x2)=loga(1+x)(1-x)=loga(1+x)-loga
,由此能求出结果.
| 1 |
| 1-x |
解答:
解:∵x2+y2=1,x>0,y>0,
且loga(1+x)=m,loga
=n,
∴logay2=loga(1-x2)=loga(1+x)(1-x)
=loga(1+x)-loga
=m-n,
故选:B.
且loga(1+x)=m,loga
| 1 |
| 1-x |
∴logay2=loga(1-x2)=loga(1+x)(1-x)
=loga(1+x)-loga
| 1 |
| 1-x |
=m-n,
故选:B.
点评:本题考查对数值的求法,是基础题,解题时要注意对数的运算性质的合理运用.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、棱柱的侧面可以是三角形 |
| B、正方体和长方体都是特殊的四棱柱 |
| C、棱柱的各条棱都相等 |
| D、所有的几何体的表面都展成平面图形 |
已知向量
、
,|
|=2,
=(3,4),
与
夹角等于60°,则
•
等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | ||||
B、
| ||||
C、5
| ||||
D、5
|
已知
=(1,-1),
=(2,3),则
•
=( )
| a |
| b |
| a |
| b |
| A、5 | B、4 | C、-2 | D、-1 |
若a,b是任意实数,且a>b,则下列不等式正确的是( )
| A、a2>b2 | ||
B、
| ||
| C、lg(a-b)>0 | ||
| D、b<a |
已知i为虚数单位,若复数z=1-i,则-
等于( )
| 1 |
| z2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):则( )
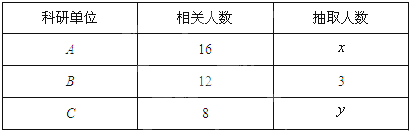

| A、x=6,y=4 |
| B、x=4,y=3 |
| C、x=7,y=4 |
| D、x=4,y=2 |
下列各式正确的是( )
A、
| |||
B、
| |||
C、
| |||
| D、a0=1 |
f(x)=3x+5,g(x)=log3(x3-5),则y=f(g(x))是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |