题目内容
6．已知数列{an}满足a1+$\frac{{a}_{2}}{2}$+$\frac{{a}_{3}}{3}$+…+$\frac{{a}_{n}}{n}$=a2n-1，求数列{an}的通项公式．分析 利用递推关系即可得出．
解答 解：∵数列{an}满足a1+$\frac{{a}_{2}}{2}$+$\frac{{a}_{3}}{3}$+…+$\frac{{a}_{n}}{n}$=a2n-1，
∴当n=1时，a1=a2-1．
当n≥2时，a1+$\frac{{a}_{2}}{2}$+$\frac{{a}_{3}}{3}$+…+$\frac{{a}_{n-1}}{n-1}$=a2（n-1）-1，
可得：$\frac{{a}_{n}}{n}$=a2n-a2n-2，
∴an=n（a2n-a2n-2），
当n=1时上式也成立，
∴an=n（a2n-a2n-2）．
点评 本题考查了数列的通项公式、递推关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
如图，四棱柱ABCD-A1B1C1D1中，平面A1ADD1⊥平面ABCD，底面ABCD为直角梯形，且∠ADC=$\frac{π}{2}$，AB∥CD．点E为棱D1D上的一点（异于点D1）．
14．已知实数a，b，c满足$\left\{\begin{array}{l}{c＞0}\\{{b}^{2}=ac}\\{3b≥2a+c}\end{array}\right.$，则$\frac{4a+2b+c}{a+b}$的最大值与最小值之和为（ ）
| A． | $\frac{15}{2}$ | B． | $\frac{13}{2}$ | C． | $\frac{31}{2}$ | D． | $\frac{51}{2}$ |
5．
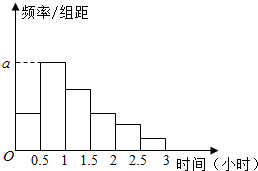随着智能手机等电子产品的普及，“低头族”正成为现代社会的一个流行词．在路上、在餐厅里、在公交车上，随处可见低头玩手机的人，这种“低头族现象”冲击了人们面对面交流的温情，也对人们的健康构成一定的影响．为此，某报社发起一项专题调查，记者随机采访了M名市民，得到这M名市民每人在一天内低头玩手机的时间（单位：小时），根据此数据作出频数的统计表和频率分布直方图如下：
（Ⅰ）求出表中的M，p及图中a的值；
（Ⅱ）试估计这M名市民在一天内低头玩手机的平均时间（同一组的数据用该组的中间值作代表）；
（Ⅲ）在所取样本中，从一天内低头玩手机的时间不少于2小时的市民中任取2人，求两人在一天内低头玩手机的时间都在区间[2，2.5）内的概率．
随着智能手机等电子产品的普及，“低头族”正成为现代社会的一个流行词．在路上、在餐厅里、在公交车上，随处可见低头玩手机的人，这种“低头族现象”冲击了人们面对面交流的温情，也对人们的健康构成一定的影响．为此，某报社发起一项专题调查，记者随机采访了M名市民，得到这M名市民每人在一天内低头玩手机的时间（单位：小时），根据此数据作出频数的统计表和频率分布直方图如下：| 分组 | 频数 | 频率 |
| [0，0.5） | 4 | 0.10 |
| [0.5，1） | m | p |
| [1，1.5） | 10 | n |
| [1.5，2） | 6 | 0.15 |
| [2，2.5） | 4 | 0.10 |
| [2.5，3） | 2 | 0.05 |
| 合计 | M | 1 |
（Ⅱ）试估计这M名市民在一天内低头玩手机的平均时间（同一组的数据用该组的中间值作代表）；
（Ⅲ）在所取样本中，从一天内低头玩手机的时间不少于2小时的市民中任取2人，求两人在一天内低头玩手机的时间都在区间[2，2.5）内的概率．