题目内容

15．某班有50名学生，一次数学考试的成绩ξ服从正态分布N（110，102），已知P（100≤ξ≤110）=0.36，估计该班学生数学成绩在120分以上的有7人．

分析 根据考试的成绩ξ服从正态分布N（110，102）．得到考试的成绩ξ关于ξ=110对称，根据P（100≤ξ≤110）=0.36，得到P（ξ≥120）=0.14，根据频率乘以样本容量得到这个分数段上的人数．

解答 解：∵考试的成绩ξ服从正态分布N（110，102）．
∴考试的成绩ξ关于ξ=110对称，
∴P=（ξ＞120）=0.5-P（100≤ξ≤110）=0.5-0.36=0.14，
所以估计该班学生数学成绩在120分以上的人数为50×0.14=7（人）．
故答案为：7．

点评 本题考查正态曲线的特点及曲线所表示的意义，是一个基础题，解题的关键是考试的成绩ξ关于ξ=110对称，利用对称写出要用的一段分数的频数，题目得解．

练习册系列答案
相关题目
5．已知函数$f（x）=\frac{lnx}{x}-\frac{k}{x}$（k∈R）的最大值为h（k）．
（1）若k≠1，试比较h（k）与$\frac{1}{{{e^{2k}}}}$的大小；
（2）是否存在非零实数a，使得$h（k）＞\frac{k}{ae}$对k∈R恒成立，若存在，求a的取值范围；若不存在，说明理由．
6．若函数f（x）满足f（x）=x（f′（x）-lnx），且f（$\frac{1}{e}$）=$\frac{1}{e}$，则ef（ex）＜f′（$\frac{1}{e}$）+1的解集是（　　）
A．（-∞，-1）B．（-1，+∞）C．（0，$\frac{1}{e}$）D．（$\frac{1}{e}$，+∞）
3．从区间（0，1）中任取两个数，作为直角三角形两直角边的长，则所得的两个数列使得斜边长不大于1的概率是（　　）
A．$\frac{π}{8}$B．$\frac{π}{4}$C．$\frac{1}{2}$D．$\frac{3}{4}$
10．已知数列$\left\{{a_n}\right\}，{a_1}=2，{a_n}=\frac{1}{n}+（{1-\frac{1}{n}}）{a_{n-1}}（{n≥2，n∈{N^*}}）$．
（1）证明：数列{nan}是等差数列；
（2）记${b_n}=\frac{1}{{{n^2}{a_n}}}$，{bn}的前n项和为Sn，证明：Sn＜1．
20．已知函数f（x）=mln（x+1）-nx在点（1，f（1））处的切线与y轴垂直，且$f'（2）=-\frac{1}{3}$，其中 m，n∈R．
（Ⅰ）求m，n的值，并求出f（x）的单调区间；
（Ⅱ）设g（x）=-x2+2x，确定非负实数a的取值范围，使不等式f（x）+x≥ag（x）在[0，+∞）上恒成立．
7．等差数列{an}中，a2=2，数列{bn}中，bn=2${\;}^{{a}_{n}}$，b4=4b2．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）若a2b1-a1b1+a3b2-a2b2+…+an+1bn-anbn≤2017，求n的最大值．
4．已知a＞0，曲线f（x）=2ax2-$\frac{1}{ax}$在点（1，f（1））处的切线的斜率为k，则当k取最小值时a的值为（　　）
A．$\frac{1}{2}$B．$\frac{2}{3}$C．1D．2
5．若函数f（x）=（ax2+bx）ex的图象如图所示，则实数a，b的值可能为（　　）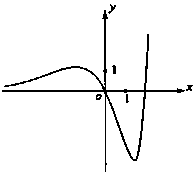
A．a=1，b=2B．a=1，b=-2C．a=-1，b=2D．a=-1，b=-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网