题目内容
如图,已知四棱锥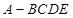 ,
,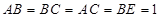 ,
,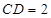 ,
,
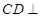 平面
平面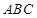 ,
,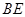 ∥
∥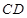 ,
,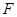 为
为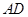 的中点.
的中点.
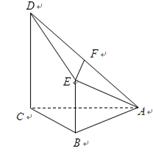
(1)求证: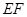 ∥平面
∥平面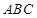 ;
;
(2)求证:平面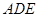
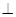 平面
平面 ;
;
(3)求四棱锥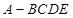 的体积.
的体积.
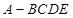 ,
,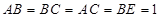 ,
,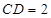 ,
,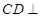 平面
平面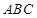 ,
,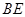 ∥
∥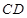 ,
,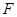 为
为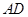 的中点.
的中点.
(1)求证:
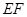 ∥平面
∥平面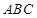 ;
;(2)求证:平面
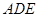
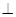 平面
平面 ;
;(3)求四棱锥
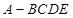 的体积.
的体积.(1)详见解析;(2)详见解析;(3)

试题分析:(1)线面平行判定定理,关键找线线平行.本题利用平行四边形找平行,取
 中点
中点 ,则易得;
,则易得; 所以四边形
所以四边形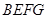 为平行四边形,即得
为平行四边形,即得 应用定理证明时,需写出定理所需条件.(2)证明面面垂直,关键证线面垂直.分析条件知,须证
应用定理证明时,需写出定理所需条件.(2)证明面面垂直,关键证线面垂直.分析条件知,须证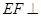 平面
平面 ,由(1)知,只需证
,由(1)知,只需证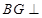 平面
平面 .因为
.因为 为等边三角形,
为等边三角形, 为
为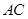 的中点 ,所以
的中点 ,所以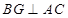 ;又可由
;又可由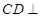 平面
平面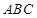 得
得 ,这样就可由线面垂直判定定理得到
,这样就可由线面垂直判定定理得到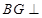 平面
平面 .(3)求三棱锥体积,关键找出高线或平面的垂线.利用面面垂直可找出面的垂线.因为
.(3)求三棱锥体积,关键找出高线或平面的垂线.利用面面垂直可找出面的垂线.因为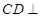 平面
平面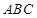 ,所以面
,所以面 平面
平面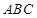 ,过A作两平面交线的垂线
,过A作两平面交线的垂线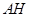 ,则有
,则有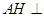 平面
平面 .因为
.因为 为等边三角形,所以
为等边三角形,所以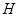 为
为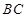 中点.
中点.试题解析:

解:(1)取
 中点
中点 ,连结
,连结 ,
, ,
,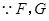 分别是
分别是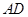 ,
, 的中点,
的中点, ∥
∥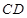 ,且
,且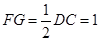 .
. ∥
∥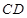 , 2分
, 2分 与
与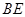 平行且相等.
平行且相等. 四边形
四边形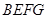 为平行四边形,
为平行四边形,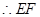 ∥
∥ . 3分
. 3分又
 平面
平面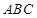 ,
, 平面
平面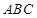 .
.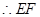 ∥平面
∥平面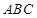 . 4分
. 4分(2)
 为等边三角形,
为等边三角形, 为
为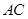 的中点,
的中点, . 5分
. 5分又
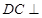 平面
平面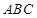 ,
, 平面
平面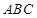 .
. , 6分
, 6分又
 ,
, 平面
平面 . 7分
. 7分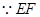 ∥
∥ ,
, 平面
平面 , 8分
, 8分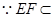 平面
平面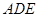 ,
, 平面
平面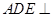 平面
平面 . 10分
. 10分(3)取
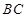 中点
中点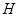 ,连结
,连结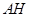 .
. ,
,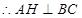 .
. 平面
平面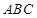 ,
, 平面
平面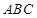
 ,
,又
 ,
,
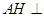 平面
平面 ,
,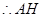 是四棱锥
是四棱锥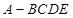 的高,且
的高,且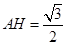 , 12分
, 12分 . 14分
. 14分
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
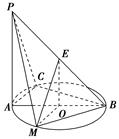
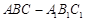 中,
中,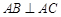 ,顶点
,顶点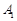 在底面
在底面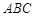 上的射影恰为点
上的射影恰为点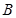 ,
,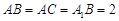 .
.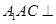 平面
平面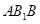 ;
; 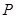 为
为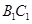 的中点,求出二面角
的中点,求出二面角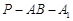 的余弦值.
的余弦值.
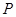 为
为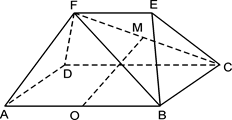
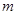 和
和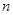 是两条不同的直线,
是两条不同的直线,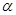 和
和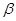 是两个不重合的平面,下面给出的条件中一定能推出
是两个不重合的平面,下面给出的条件中一定能推出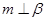 的是( )
的是( )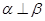 且
且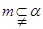
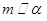
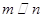 且
且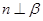
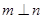 且
且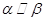
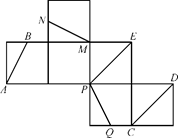
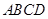 沿对角线
沿对角线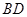 折成直二面角
折成直二面角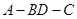 ,有如下四个结论:
,有如下四个结论: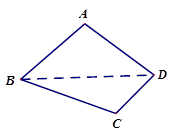
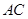 ⊥
⊥ 是等边三角形;
是等边三角形;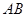 与
与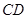 所成的角为60°;
所成的角为60°;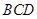 所成的角为60°.
所成的角为60°.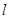 不平行于平面
不平行于平面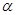 ,且
,且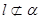 ,则( )
,则( ) 中,过对角线
中,过对角线 的一个平面交棱
的一个平面交棱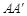 于E,交棱
于E,交棱 于F,则:①四边形
于F,则:①四边形 一定是平行四边形;②四边形
一定是平行四边形;②四边形 .
.