题目内容
对于任意x,[x]表示不超过x的最大整数,如[1,1]=1[-2,1]=-3,定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤1},则A中所有元素的和为
- A.55
- B.58
- C.63
- D.65
B
分析:根据新定义,[x]表示不超过x的最大整数,要求y=f(x)=[2x]+[4x]+[8x],需要分类讨论有几个界点x= ,
,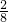 ,
, ,••
,•• ,对其进行讨论,从而进行求解;
,对其进行讨论,从而进行求解;
解答:∵任意x,[x]表示不超过x的最大整数,如[1,1]=1[-2,1]=-3,定义R上的函数f(x)=[2x]+[4x]+[8x],
若A={y|y=f(x),0≤x≤1},
当 ,0≤2x<
,0≤2x< ,0≤4x<
,0≤4x< ,0≤8x<1,f(x)=[2x]+[4x]+[8x]=0;
,0≤8x<1,f(x)=[2x]+[4x]+[8x]=0;
当 ,
, ≤2x<
≤2x< ,
, ≤4x<1,1≤8x<2,f(x)=[2x]+[4x]+[8x]=1;
≤4x<1,1≤8x<2,f(x)=[2x]+[4x]+[8x]=1;
当 ,
, ≤2x<
≤2x< ,1≤4x<
,1≤4x< ,2≤8x<3,f(x)=[2x]+[4x]+[8x]=0+1=2=3;
,2≤8x<3,f(x)=[2x]+[4x]+[8x]=0+1=2=3;
当 ,
, ≤2x<1,
≤2x<1, ≤4x<2,3≤8x<4,f(x)=[2x]+[4x]+[8x]=0+1+3=4;
≤4x<2,3≤8x<4,f(x)=[2x]+[4x]+[8x]=0+1+3=4;
当 ,1≤2x<
,1≤2x< ,2≤4x<
,2≤4x< ,4≤8x<5,f(x)=[2x]+[4x]+[8x]=1+2+4=7;
,4≤8x<5,f(x)=[2x]+[4x]+[8x]=1+2+4=7;
当 ,
, ≤2x<
≤2x< ,
, ≤4x<3,5≤8x<6,f(x)=[2x]+[4x]+[8x]=1+2+5=8;
≤4x<3,5≤8x<6,f(x)=[2x]+[4x]+[8x]=1+2+5=8;
当 ,
, ≤2x<
≤2x< ,3≤4x<
,3≤4x< ,6≤8x<7,f(x)=[2x]+[4x]+[8x]=1+3+6=10;
,6≤8x<7,f(x)=[2x]+[4x]+[8x]=1+3+6=10;
当 ,
, ≤2x<2,
≤2x<2, ≤4x<4,7≤8x<8,f(x)=[2x]+[4x]+[8x]=1+3+7=11;
≤4x<4,7≤8x<8,f(x)=[2x]+[4x]+[8x]=1+3+7=11;
f(1)=2+4+8=14;
所以A中所有元素的和为0+1+3+4+7+8+10+11+14=58;
故选B;
点评:此题主要考查函数的值,需要分类进行讨论,新定义一般需要认真读题,理解题意,是一道基础题;
分析:根据新定义,[x]表示不超过x的最大整数,要求y=f(x)=[2x]+[4x]+[8x],需要分类讨论有几个界点x=
 ,
,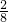 ,
, ,••
,•• ,对其进行讨论,从而进行求解;
,对其进行讨论,从而进行求解;解答:∵任意x,[x]表示不超过x的最大整数,如[1,1]=1[-2,1]=-3,定义R上的函数f(x)=[2x]+[4x]+[8x],
若A={y|y=f(x),0≤x≤1},
当
 ,0≤2x<
,0≤2x< ,0≤4x<
,0≤4x< ,0≤8x<1,f(x)=[2x]+[4x]+[8x]=0;
,0≤8x<1,f(x)=[2x]+[4x]+[8x]=0;当
 ,
, ≤2x<
≤2x< ,
, ≤4x<1,1≤8x<2,f(x)=[2x]+[4x]+[8x]=1;
≤4x<1,1≤8x<2,f(x)=[2x]+[4x]+[8x]=1;当
 ,
, ≤2x<
≤2x< ,1≤4x<
,1≤4x< ,2≤8x<3,f(x)=[2x]+[4x]+[8x]=0+1=2=3;
,2≤8x<3,f(x)=[2x]+[4x]+[8x]=0+1=2=3;当
 ,
, ≤2x<1,
≤2x<1, ≤4x<2,3≤8x<4,f(x)=[2x]+[4x]+[8x]=0+1+3=4;
≤4x<2,3≤8x<4,f(x)=[2x]+[4x]+[8x]=0+1+3=4;当
 ,1≤2x<
,1≤2x< ,2≤4x<
,2≤4x< ,4≤8x<5,f(x)=[2x]+[4x]+[8x]=1+2+4=7;
,4≤8x<5,f(x)=[2x]+[4x]+[8x]=1+2+4=7;当
 ,
, ≤2x<
≤2x< ,
, ≤4x<3,5≤8x<6,f(x)=[2x]+[4x]+[8x]=1+2+5=8;
≤4x<3,5≤8x<6,f(x)=[2x]+[4x]+[8x]=1+2+5=8;当
 ,
, ≤2x<
≤2x< ,3≤4x<
,3≤4x< ,6≤8x<7,f(x)=[2x]+[4x]+[8x]=1+3+6=10;
,6≤8x<7,f(x)=[2x]+[4x]+[8x]=1+3+6=10;当
 ,
, ≤2x<2,
≤2x<2, ≤4x<4,7≤8x<8,f(x)=[2x]+[4x]+[8x]=1+3+7=11;
≤4x<4,7≤8x<8,f(x)=[2x]+[4x]+[8x]=1+3+7=11;f(1)=2+4+8=14;
所以A中所有元素的和为0+1+3+4+7+8+10+11+14=58;
故选B;
点评:此题主要考查函数的值,需要分类进行讨论,新定义一般需要认真读题,理解题意,是一道基础题;

练习册系列答案
相关题目
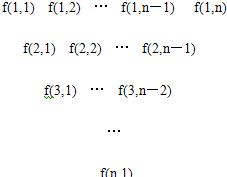 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j). ,
, ,设
,设 1,
1, 




 ,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为( )
,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为( )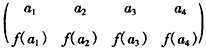 ,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为
,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为