题目内容
19.设$\overrightarrow{i}$,$\overrightarrow{j}$分别为直角坐标系中Ox,Oy正方向上的单位向量,设$\overrightarrow{OA}$=-2$\overrightarrow{i}$+m$\overrightarrow{j}$,$\overrightarrow{OB}$=n$\overrightarrow{i}$+$\overrightarrow{j}$,$\overrightarrow{OC}$=5$\overrightarrow{i}$-$\overrightarrow{j}$,若点A,B,C在一条直线上,且m-2n=0,则m的值是( )| A. | 1或2 | B. | 1或3 | C. | 2或3 | D. | 3或6 |
分析 由已知条件求出$\overrightarrow{OA}=(-2,m),\overrightarrow{OB}=(n,1)$,$\overrightarrow{OC}=(5,-1)$,而由A,B,C三点共线便知,存在实数k使得:$\overrightarrow{AB}=k\overrightarrow{AC}$,从而得到$\overrightarrow{OB}-\overrightarrow{OA}=k(\overrightarrow{OC}-\overrightarrow{OA})$,带入向量坐标便可得到(n+2,1-m)=k(7,-(1+m)).从而得到$n=\frac{5m-9}{1+m}$,带入已知的m-2n=0中,便可解出m.
解答 解:根据条件,$\overrightarrow{OA}=(-2,m),\overrightarrow{OB}=(n,1),\overrightarrow{OC}=(5,-1)$;
A,B,C三点在一条直线上;
∴$\overrightarrow{AB}=k\overrightarrow{AC}$;
∴$\overrightarrow{OB}-\overrightarrow{OA}=k(\overrightarrow{OC}-\overrightarrow{OA})$;
∴(n,1)-(-2,m)=k[(5,-1)-(-2,m)];
∴(n+2,1-m)=(7k,-k(1+m));
∴$\left\{\begin{array}{l}{n+2=7k}\\{1-m=-k(1+m)}\end{array}\right.$,消去k得:7m-7=(n+2)(1+m);
∴n=$\frac{5m-9}{1+m}$,带入m-2n=0得,$m-\frac{10m-18}{1+m}=0$;
解得m=3,或6.
故选:D.
点评 考查向量坐标的定义,共线向量基本定理,向量减法的几何意义,以及向量坐标的减法及数乘运算.

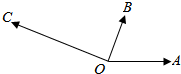 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )| A. | x=-2,y=-1 | B. | x=-2,y=1 | C. | x=2,y=-1 | D. | x=2,y=1 |
| A. | 0 | B. | -1 | C. | ±1 | D. | 1 |