题目内容

在△ABC中，
AN
=
1
3
NC
，P是BN上的一点，若
AP
=m
AB
+
2
11
AC
，则实数m的值为
3
11
3
11
．
分析：设
BP
=λ
BN
，我们易将
AP
表示为（1-λ）
AB
+
λ
4
AC
的形式，根据平面向量的基本定理我们易构造关于λ，m的方程组，解方程组后即可得到m的值．
解答：解：∵P是BN上的一点，
设
BP
=λ
BN
，由
AN
=
1
3
NC
，
则
AP
=
AB
+
BP

=
AB
+λ
BN

=
AB
+λ（
AN
-
AB
）
=（1-λ）
AB
+λ
AN

=（1-λ）
AB
+
λ
4
AC

∴m=1-λ，
λ
4
=
2
11

解得λ=
8
11
，m=
3
11

故答案为：
3
11
．
点评：本题主要考查了的知识点是面向量的基本定理及其意义，解答本题的关键是根据面向量的基本定理构造关于λ，m的方程组，属于中档题．
练习册系列答案
相关题目
精英家教网如图，在△ABC中，
AN
=
1
3
NC
，P是BN上的一点，若
AP
=m
AB
+
2
11
AC
，则实数m的值为
 
．
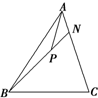给出下列三个命题：
①函数y=
1
2
ln
1-cos x
1+cos x
与y=lntan
x
2
是同一函数；
②若函数y=f（x）与y=g（x）的图象关于直线y=x对称，则函数y=f（2x）与y=
1
2
g（x）的图象也关于直线y=x对称；
③如图，在△ABC中，
AN
=
1
3
NC
，P是BN上的一点，若
AP
=m
AB
+
2
11
AC
，则实数m的值为
3
11
．
其中真命题是（　　）
（2013•石家庄二模）如图，在△ABC中，
AN
=
1
2
NC
，P是BN上的一点，若
AP
=m
AB
+
2
9
AC
，则实数m的值为（　　）
在△ABC中，
AN
=
1
2
NC
，P是BN的中点，用
AB
，
AC
表示
AP
，
AP
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网