题目内容
在△ABC中,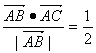 ,
,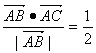 ,又E点在BC边上,且满足
,又E点在BC边上,且满足(1)求此双曲线的方程;
(2)设P是此双曲线上任意一点,过A点作∠APB平分线的垂线,垂足为M,求M点的轨迹方程.
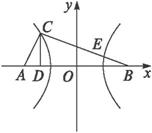
解:(1)以线段AB的中点O为原点,直线AB为x轴建立平面直角坐标系,如图

∴A(-1,0),B(1,0),
作CD⊥AB于D,由已知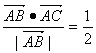 ,∴
,∴![]() cosA=
cosA=![]() ,即
,即![]() =
=![]() ,
,
同理又∵ ,∴
,∴![]() ,
,
设双曲线的方程为![]() =1(a>0,b>0),C(-
=1(a>0,b>0),C(-![]() ,h),E(x1,y1),
,h),E(x1,y1),
又![]() ,∴
,∴ 又E、C两点在双曲线上,
又E、C两点在双曲线上,
∴ 解得a2=
解得a2=![]() ,
,
∴b2=![]()
∴双曲线方程为7x2-![]() y2=1.
y2=1.
(2)设AM的延长线或延长线交PB于N点,则△PAN是等腰三角形,|PA|=|PN|且M是AN的中点,
∴|OM|=![]() |NB|=
|NB|=![]() ||PB|-|PN||=||PB|-|PA||=a,
||PB|-|PN||=||PB|-|PA||=a,
∴M点的轨迹是以O为圆心,以a为半径的圆,∴方程为x2+y2=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
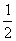 =
=