题目内容
如图，在△ABC中，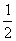
=
，
=
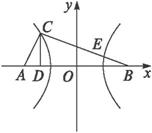
，又E在BC边上，且满足3
=2
，若以A，B为焦点的双曲线过C，E两点，求此双曲线的方程.
思路解析：可设出C、E的坐标，由已知条件以及C、E在双曲线上，联立方程组求解. 解：以线段AB的中点O为原点，直线AB为x轴，建立直角坐标系，作CD⊥AB于D，由已知得| ∴| 设双曲线方程为 得3（x0-1,y0）=2(- 因为E，C在双曲线上，所以 得a2= 所以双曲线方程为7x2- 方法归纳 当已知曲线的形状求轨迹时，往往采用待定系数，当然，它可以与其他方法结合使用.
|=，||=，|=2，则A（-1，0），B（1，0）.-=1及C（-
，h），E（x0,y0）,由3BE=2EC，
-x0,h-y0)
∴E（
，
）.
,b2=c2-a2=1-
=
,
y2=1.
练习册系列答案
三维同步学与练系列答案
毕业复习指导与训练系列答案
中考试题荟萃及详解系列答案
尚文阅读系列答案
深圳市小学第1课堂系列答案
深圳市小学英语课堂跟踪系列答案
神奇图解小学英语阅读100篇系列答案
升学锦囊系列答案
师说系列答案
实验班培优训练系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知