��Ŀ����
8����֪����C1�ļ����귽��Ϊ��2cos2��=18������C2�ļ����귽��Ϊ��=$\frac{��}{6}$������C1��C2�ཻ��A��B���㣮��1����A��B����ļ����ꣻ
��2������C1��ֱ��$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$��tΪ�������ֱ��ཻ��M��N���㣬���߶�MN�ij��ȣ�
���� ��1���ɦ�=$\frac{��}{6}$�������2cos2��=18���ɵæ�=��6�������õ���A��B�ļ����꣮
��2��������C1�ļ����귽�̦�2cos2��=18��Ϊ��2��cos2��-sin2�ȣ�=18�����ɵõ���ͨ����Ϊx2-y2=18����ֱ��$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$����x2-y2=8��������${t}^{2}+4\sqrt{3}t-28=0$�������õ�|MN|��
��� �⣺��1����=$\frac{��}{6}$�������2cos2��=18���ɵæ�=��6��
��A��B����ļ�����ֱ�Ϊ��6��$\frac{��}{6}$������-6��$\frac{��}{6}$����
��2������C1�ļ����귽��Ϊ��2cos2��=18����Ϊ��2��cos2��-sin2�ȣ�=18��
�õ�ֱ�����귽��Ϊx2-y2=18��
ֱ��$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$����x2-y2=18��
������${t}^{2}+4\sqrt{3}t-28=0$��
��|MN|=$\sqrt{��-4\sqrt{3}��^{2}-4����-28��}$=4$\sqrt{10}$��
���� ���⿼���˼�������ֱ������Ļ�����ʽ���������̻�Ϊ��ͨ���̡��ҳ���ʽ�Ȼ���֪ʶ��������ܷ�����

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�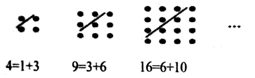 ��ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10��15��������������Ϊ������������������1��4��9��16��25��������������Ϊ������������������ͼ�п��Է��֣��κ�һ������1�ġ����������������Կ����������ڡ�����������֮�ͣ����е�ʽ�У�������һ���ɵ��ǣ�������
��ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10��15��������������Ϊ������������������1��4��9��16��25��������������Ϊ������������������ͼ�п��Է��֣��κ�һ������1�ġ����������������Կ����������ڡ�����������֮�ͣ����е�ʽ�У�������һ���ɵ��ǣ�������| A�� | 16=3+13 | B�� | 25=9+16 | C�� | 36=10+26 | D�� | 49=21+28 |

| ���� | ���� | ��̼������� | ռ�����Ƶ�� |
| ��һ�� | [25��30�w | 120 | 0.6 |
| �ڶ��� | [30��35�w | 195 | p |
| ������ | [35��40�w | 100 | 0.5 |
| ������ | [40��45�w | a | 0.4 |
| ������ | [45��50�w | 30 | 0.3 |
| ������ | [50��55] | 15 | 0.3 |
�����������[40��50���ġ���̼�塱�в��÷ֲ��������ȡ6�˲μӻ����̼����������ѡȡ2����Ϊ��ӣ���ѡȡ��2�������ǡ��1��������[40��45����ĸ��ʣ�
| A�� | ��m��n��n?������m�� | B�� | ��l��n��m��n����l��m | ||
| C�� | ��l�ͦ���m�ͦ£���l��m������ͦ� | D�� | �����ͦ£����ɦ�=m����m��n����n�ͦ� |
| A�� | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B�� | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C�� | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D�� | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
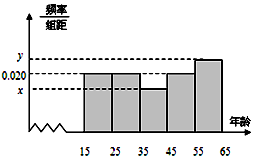 ij���Ļ�����Ϊ���˽Ȿ������Ե��صط�Ϸ���Ƿ�ϲ������15-65�����Ⱥ�����������n�ˣ��õ����µ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ��
ij���Ļ�����Ϊ���˽Ȿ������Ե��صط�Ϸ���Ƿ�ϲ������15-65�����Ⱥ�����������n�ˣ��õ����µ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ������д�����е�a��b��n��x��y��ֵ��
�������ӵ�1��2��3��ش�ϲ���ط�Ϸ���������÷ֲ�����ķ�����ȡ6�ˣ���������ÿ��ֱ��ȡ�����ˣ�
�����ڣ���ȡ��6���������ȡ2�ˣ���X��ʾ�����ǵ�3�����������X�ķֲ��к�������
| ��� | ���� | ϲ������ | ϲ������ռ�����Ƶ�� |
| ��1�� | [15��25�� | a | 0.10 |
| ��2�� | [25��35�� | b | 0.20 |
| ��3�� | [35��45�� | 6 | 0.40 |
| ��4�� | [45��55�� | 12 | 0.60 |
| ��5�� | [55��65�� | 20 | 0.80 |
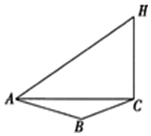 ij�̻�����Ϊ�˲����������Ƴ���һ�֡����족��Ʒ���յİ�ȫ�ԣ��ض��������һ����ԣ���ͼ�������̻���ȼ�ŵ�C����ȼ��ʵ�飬������Ա�ס��ҷֱ���A��B���أ�����������ͬһˮƽ���ϣ���������Ա�ײ��A��B�������80���ҡ�BAC=60�㣬�������̻�ȼ�š����족ʱ��������ʱ�������$\frac{1}{17}$�룮��A�ز�ø��̻�������ߵ�H��������Ϊ60�㣮����֪�����Ĵ����ٶ�Ϊ340�רM�룩
ij�̻�����Ϊ�˲����������Ƴ���һ�֡����족��Ʒ���յİ�ȫ�ԣ��ض��������һ����ԣ���ͼ�������̻���ȼ�ŵ�C����ȼ��ʵ�飬������Ա�ס��ҷֱ���A��B���أ�����������ͬһˮƽ���ϣ���������Ա�ײ��A��B�������80���ҡ�BAC=60�㣬�������̻�ȼ�š����족ʱ��������ʱ�������$\frac{1}{17}$�룮��A�ز�ø��̻�������ߵ�H��������Ϊ60�㣮����֪�����Ĵ����ٶ�Ϊ340�רM�룩