题目内容
18.(x-y)(x+2y+z)6的展开式中,x2y3z2的系数为( )| A. | -30 | B. | 120 | C. | 240 | D. | 420 |
分析 (x+2y+z)6的展开式的通项公式:Tr+1=${∁}_{6}^{r}$(2y)6-r(x+z)r=26-r${∁}_{6}^{r}$y6-r(x+z)r,(x+z)r的展开式的通项公式:Tk+1=${∁}_{r}^{k}$xr-kzk.可得两个通项公式相乘可得展开式的通项形式:26-r${∁}_{6}^{r}$y6-r•${∁}_{r}^{k}$xr-kzk.通过分类讨论即可得出.
解答 解:(x+2y+z)6的展开式的通项公式:Tr+1=${∁}_{6}^{r}$(2y)6-r(x+z)r=26-r${∁}_{6}^{r}$y6-r(x+z)r,
(x+z)r的展开式的通项公式:Tk+1=${∁}_{r}^{k}$xr-kzk.
可得两个通项公式相乘可得展开式的通项形式:26-r${∁}_{6}^{r}$y6-r•${∁}_{r}^{k}$xr-kzk.
令r-k+1=2,6-r=3,k=2,或r-k=2,6-r+1=3,k=2.
解得k=2,r=3.或k=2,r=4.
∴x2y3z2的系数为${2}^{3}{∁}_{6}^{3}{∁}_{3}^{2}$-${2}^{2}{∁}_{6}^{4}{∁}_{4}^{2}$=120.
故选:B.
点评 本题考查了二项式定理的应用、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.某几何体的三视图如图,则该几何体的体积是( )
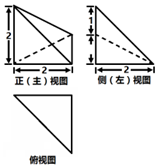

| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 2 |
13.函数f(x)=$\frac{{sinx\sqrt{1-|x|}}}{{|{x+2}|-2}}$的奇偶性是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
10.某校为了了解1200名学生对高效课堂试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为( )
| A. | 30 | B. | 25 | C. | 20 | D. | 12 |
8.在△ABC中,若sinA:sinB:sinC=2:3:4,则最大角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |