题目内容
18.已知抛物线C:y2=4x的焦点F,点P为抛物线C上任意一点,若点A(3,1),则|PF|+|PA|的最小值为4.分析 设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|PA|+|PD|取得最小,进而可推断出当D,P,A三点共线时|PA|+|PD|最小,答案可得.
解答  解:抛物线C:y2=4x的准线为x=-1.
解:抛物线C:y2=4x的准线为x=-1.
设点P在准线上的射影为D,
则根据抛物线的定义可知|PF|=|PD|,
要求|PA|+|PF|取得最小值,即求|PA|+|PD|取得最小.
当D,P,A三点共线时,|PA|+|PD|最小,为3-(-1)=4.
故答案为:4.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,判断当D,P,A三点共线时|PA|+|PD|最小,是解题的关键.

练习册系列答案
相关题目
6.定义域为D的单调函数y=f(x),如果存在区间[m,n]⊆D,满足当定义域为是[m,n]时,f(x)的值域也是[m,n],则称[m,n]是该函数的“可协调区间”;如果函数y=$\frac{({a}^{2}+a)x-1}{{a}^{2}x}$(a≠0)的一个可协调区间是[m,n],则实数a的取值范围是( )
| A. | -3<a<1 | B. | -3<a<0 | C. | 0<a<1 | D. | a<-3或a>1 |
6.已知抛物线y2=8x的焦点为F,过点F作直线交抛物线于点A,B,点M为AB的中点,过点M作准线的垂线,交抛物线于点P,若|FP|=$\frac{5}{2}$,则|AB|=( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
13.已知角α的终边经过点A(-$\sqrt{3}$,a),若点A在抛物线y=-$\frac{1}{4}$x2的准线上,则sinα=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
8.把一枚硬币任意抛掷三次,事件A=“至少一次出现正面”,事件B“恰有一次出现正面”,则P(B|A)=( )
| A. | $\frac{3}{7}$ | B. | $\frac{3}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{8}$ |
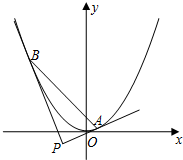 已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.
已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.