题目内容

函数y=Asin（ωx+?）（ω＞0，A≠0）的图象与函数y=Acos（ωx+?）（ω＞0，A≠0）的图象在区间（x0，x0+
π
ω
）上（　　）
A．至少有两个交点B．至多有两个交点
C．至多有一个交点D．至少有一个交点
两个函数的图象可知在一个周期内有两个交点，两个交点之间的距离是半周期，而区间（x0，x0+
π
ω
）
相差小于半周期，所以函数y=Asin（ωx+?）（ω＞0，A≠0）的图象与函数y=Acos（ωx+?）（ω＞0，A≠0）的图象在区间（x0，x0+
π
ω
）上至多有一个交点．
故选C．
练习册系列答案
相关题目
若函数y=Asin（ωx+φ）（ω＞0）与x轴的两个相邻的交点坐标为（-4，0），（2，0），则ω=
 
．
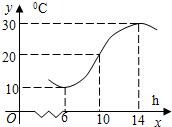精英家教网如图所示，某地一天从6时到14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，则8时的温度大约为
 
°C（精确到1°C）
已知函数y=Asin（ωx+φ）+C（A＞0，ω＞0，|φ|＜
π2
）在同一周期中最高点的坐标为（2，2），最低点的坐标为（8，-4）．
（I）求A，C，ω，φ的值；
（II）求出这个函数的单调递增区间．
如图，是函数y=Asin（ωx+φ），（-π＜φ＜π）的图象的一段，O是坐标原点，P是图象的最高点，A点坐标为（5，0），若|
OP
|=
10
，
OP
•
OA
=15，则此函数的解析式为
y=sin(
π
4
x-
π
4
)
y=sin(
π
4
x-
π
4
)
．
已知：函数y=Asin（ωx+φ），在同一周期内，当x=
π
12
时取最大值y=4；当x=
7π
12
时，取最小值y=-4，那么函数的解析式为：（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网