题目内容
已知两定点 ,直线l过点A且与直线
,直线l过点A且与直线 平行,则l上满足||PA|-|PB||=2的点P的个数为( )
平行,则l上满足||PA|-|PB||=2的点P的个数为( )A.0
B.1
C.2
D.无法确定
【答案】分析:由题意得直线l的方程为 双曲线的方程为
双曲线的方程为 ,点P在l上且满足||PA|-|PB||=2因为双曲线的渐近线y=±
,点P在l上且满足||PA|-|PB||=2因为双曲线的渐近线y=± 与直线l平行所以结合着图形得直线l与双曲线的交点只有一个,即l上满足||PA|-|PB||=2的点P的个数为1
与直线l平行所以结合着图形得直线l与双曲线的交点只有一个,即l上满足||PA|-|PB||=2的点P的个数为1
解答:解:∵直线l过点A且与直线 平行
平行
∴直线l的方程为
由题意可得若点P满足||PA|-|PB||=2
则点P在以 为焦点以2为实轴,以
为焦点以2为实轴,以 为虚轴的双曲线上
为虚轴的双曲线上
即双曲线的方程为
由题意得点P在l上且满足||PA|-|PB||=2
∴点P为直线l与双曲线的交点
∵双曲线的渐近线y=± 与直线l平行
与直线l平行
∴直线l与双曲线的交点只有一个
∴l上满足||PA|-|PB||=2的点P的个数为1
故答案为B
点评:本题考查双曲线方程的求解以及直线与双曲线的位置关系,在判断位置关系时要特别注意直线与双曲线渐近线的关系.
 双曲线的方程为
双曲线的方程为 ,点P在l上且满足||PA|-|PB||=2因为双曲线的渐近线y=±
,点P在l上且满足||PA|-|PB||=2因为双曲线的渐近线y=± 与直线l平行所以结合着图形得直线l与双曲线的交点只有一个,即l上满足||PA|-|PB||=2的点P的个数为1
与直线l平行所以结合着图形得直线l与双曲线的交点只有一个,即l上满足||PA|-|PB||=2的点P的个数为1解答:解:∵直线l过点A且与直线
 平行
平行∴直线l的方程为

由题意可得若点P满足||PA|-|PB||=2

则点P在以
 为焦点以2为实轴,以
为焦点以2为实轴,以 为虚轴的双曲线上
为虚轴的双曲线上即双曲线的方程为

由题意得点P在l上且满足||PA|-|PB||=2
∴点P为直线l与双曲线的交点
∵双曲线的渐近线y=±
 与直线l平行
与直线l平行∴直线l与双曲线的交点只有一个
∴l上满足||PA|-|PB||=2的点P的个数为1
故答案为B
点评:本题考查双曲线方程的求解以及直线与双曲线的位置关系,在判断位置关系时要特别注意直线与双曲线渐近线的关系.

练习册系列答案
相关题目
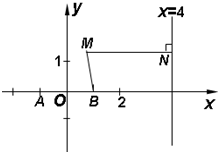 如图,已知两定点A(-1,0),B(1,0)和定直线l:x=4,动点M在直线l上的射影为N,且
如图,已知两定点A(-1,0),B(1,0)和定直线l:x=4,动点M在直线l上的射影为N,且 ,直线l过点A且与直线
,直线l过点A且与直线 平行,则l上满足||PA|-|PB||=2的点P的个数为
平行,则l上满足||PA|-|PB||=2的点P的个数为 ,直线l过点A且与直线
,直线l过点A且与直线 平行,则l上满足||PA|-|PB||=2的点P的个数为( )
平行,则l上满足||PA|-|PB||=2的点P的个数为( )