Question

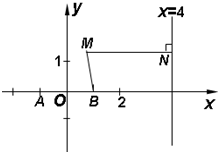如图，已知两定点A（-1，0），B（1，0）和定直线l：x=4，动点M在直线l上的射影为N，且2|

BM

|=|

MN

|．
（Ⅰ）求动点M的轨迹C的方程并画草图；
（Ⅱ）是否存在过点A的直线n，使得直线n与曲线C相交于P，Q两点，且△PBQ的面积等于

6 3

5

？如果存在，请求出直线n的方程；如果不存在，请说明理由．

Answer 1

分析：（Ⅰ）用两点间距离公式分别求|

BM

|，|

MN

|，再代入2|

BM

|=|

MN

|，化简，即可得动点M的轨迹C的方程，再根据方程画出图形即可．
（Ⅱ）先假设存在过点A的直线n，使得直线n与曲线C相交于P，Q两点，且△PBQ的面积等于

6 3

5

，分斜率存在和斜率不存在两种情况设出直线n的方程，与曲线C的方程联立，求出△PBQ的面积，让面积等于

6 3

5

，解k，若能解出，则存在，若解不出，则不存在．

解答：解：（Ⅰ）设M（x，y），则|

BM

|=

(x-1)2+y2

，|

MN

|=|x-4|，代入2|

BM

|=|

MN

|，得2

(x-1)2+y2

=|x-4|，化简得，
即得曲线C的方程为

x2

4

+

y2

3

=1，
草图如图所示．
（Ⅱ）（i）若直线n的斜率不存在时，此时点P(-1 ，- 

3

2

)，点Q(-1 ， 

3

2

)，△PBQ的面积等于3，不符合；
（ii）若直线n的斜率为k时，直线n的方程设为y=k（x+1），设P（x₁，y₁），Q（x₂，y₂）．
联立

y=k(x+1) x2 4 + y2 3 =1

，得(

1

4

+

1

3

k2)x2+

2

3

k2x+

1

3

k2-1=0，则x1+x2=-

8k2

3+4k2

，x1x2=

4k2-12

3+4k2

，则|x1-x2|=

(x1+x2)2-4x1x2

=

12 k2+1

3+4k2

，
所以 |PQ|=

1+k2

|x1-x2|=

12(1+k2)

3+4k2

，
点B到直线n的距离d=

|2k|

k2+1

，
所以△PBQ的面积等于

1

2

•

12(1+k2)

3+4k2

•

2|k|

1+k2

=

6 3

5

，解之得：k=±

2

2

，
故存在直线n为y=±

2

2

(x+1)．

点评：本题考查了椭圆方程的求法，以及存在性问题的解法，做题时要认真分析．