题目内容
已知实数x,y满足约束条件
且目标函数z=2x+y的最大值是6,最小值是1,则
的值是( )
|
| c |
| b |
| A、1 | B、2 | C、3 | D、4 |
考点:简单线性规划
专题:不等式的解法及应用
分析:先根据约束条件画出可行域,再利用目标函数的最值,作用平面区域即可得到结论..
解答:
解:由题意得: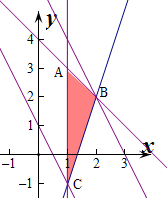
作出目标函数2x+y=6,和2x+y=1,
则对应的平面区域如图:
则B,C在直线ax+by+c=0上,
由
,解得
,即C(1,-1),
由
,解得
,即B(2,2),
则B,C在直线在直线ax+by+c=0上,
∴BC的方程为3x-y-4=0,
即a=3,b=-1,c=-4,
则
=4,
故选:D

作出目标函数2x+y=6,和2x+y=1,
则对应的平面区域如图:
则B,C在直线ax+by+c=0上,
由
|
|
由
|
|
则B,C在直线在直线ax+by+c=0上,
∴BC的方程为3x-y-4=0,
即a=3,b=-1,c=-4,
则
| c |
| b |
故选:D
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数y=2x图象上存在点(x,y)满足约束条件
,则实数m的最大值为( )
|
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
为了得到函数y=cos2x-sin2x的图象,可以将函数y=
cos2x的图象( )
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
等差数列{an}满足a2=4,a1+a4+a7=24,则a10=( )
| A、16 | B、18 | C、20 | D、22 |
设Sn为等差数列{an}(n∈N+)的前n项和,且S2=S6,a4=1,则a5=( )
| A、-1 | B、0 | C、1 | D、2 |
在平面直角坐标系中,A(0,0),B(1,2)两点绕定点P顺时针旋转θ角分别到A′(4,4),B′(5,2)两点,则cosθ的值为( )
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
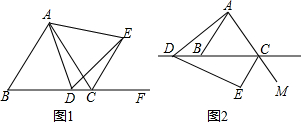 如图1所示,点D是等边三角形ABC的边BC上一点,连结AD作∠ADE=60°,交∠ABC的外角平分线CE于E
如图1所示,点D是等边三角形ABC的边BC上一点,连结AD作∠ADE=60°,交∠ABC的外角平分线CE于E