题目内容
若函数f（x）=mx-1+1（m，0，且m≠1）恒过定点A，而点A恰好在直线2ax+by-2=0上（其中a，0，b，0）则式子
+
的最小值为______．
| 1 |
| a |
| 4 |
| b |
函数f（x）=mx-1+1（m，0，且m≠1）恒过定点A（1，2），而点A恰好在直线2ax+by-2=0上，
∴2a+2b-2=0，即 a+b=1，∴
+
=
+
=5+
+
≥5+2
=9，
当且仅当
=
时，取等号．
故答案为：9．
∴2a+2b-2=0，即 a+b=1，∴
| 1 |
| a |
| 4 |
| b |
| a+b |
| a |
| 4a+4b |
| b |
| b |
| a |
| 4a |
| b |
| 4 |
当且仅当
| b |
| a |
| 4a |
| b |
故答案为：9．
练习册系列答案
相关题目
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．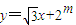
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．