题目内容
8.已知f1(x)=ex(sinx+cosx),fn+1(x)=fn′(x),则f2017(x)=( )| A. | -21007excosx | B. | -21007ex(cosx-sinx) | ||
| C. | 21008exsinx | D. | 21008ex(sinx+cosx) |
分析 求函数的导数,寻找导函数的规律即可得到结论.
解答 解:f2(x)=f1′(x)=ex(sinx+cosx)+ex(cosx-sinx)=2ex•cosx,
f3(x)=f2′(x)=2ex•(cosx-sinx),
f4(x)=f3′(x)=-22ex•sinx,
f5(x)=f4′(x)=-22ex(sinx+cosx),
f6(x)=f5′(x)=-23excosx,
f7(x)=f6′(x)=-23ex(cosx-sinx),
f8(x)=f7′(x)=24exsinx,
f9(x)=f8′(x)=24ex(sinx+cosx)
…
f2017(x)=21008ex(sinx+cosx),
故选:D
点评 本题考查三角函数的导数、周期性、及观察归纳思想的运用,属于中档题.熟练掌握三角函数的求导法则,利用其中的函数周期性则解决本题的关键.

练习册系列答案
相关题目
10.已知{an}是等比数列,其中a1,a8是关于x的方程x2-2xsinα-$\sqrt{3}$sinα=0的两根,且(a1+a8)2=2a3a6+6,则锐角α的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
8.已知$\overline z$是z的共轭复数,且|z|-$\overline z$=3+4i,则z的虚部是( )
| A. | $\frac{7}{6}$ | B. | $-\frac{7}{6}$ | C. | 4 | D. | -4 |
17.某几何体的三视图如图,它的侧视图与正视图相同,则它的体积为( )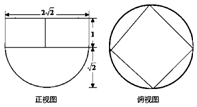

| A. | $2+\frac{{4\sqrt{2}π}}{3}$ | B. | $4+\frac{{8\sqrt{2}π}}{3}$ | C. | $2+\frac{{8\sqrt{2}π}}{3}$ | D. | $4+\frac{{4\sqrt{2}π}}{3}$ |
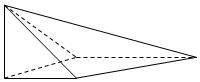 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.