题目内容
1.已知F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点,A,B为椭圆C的左、右顶点,点P在椭圆C上,且PF⊥x轴,过点A的直线与线段PF交与点M,与y轴交与点E,直线BM与y轴交于点N,若NE=2ON,则椭圆C的离心率为$\frac{1}{2}$.分析 由题意可得F,A,B的坐标,设出直线AE的方程为y=k(x+a),分别令x=-c,x=0,可得M,E的坐标,再由直线BM与y轴交于点N,NE=2ON,可得N的坐标,运用三点共线的条件:斜率相等,结合离心率公式,即可得到所求值.
解答 解:由题意可设F(-c,0),A(-a,0),B(a,0),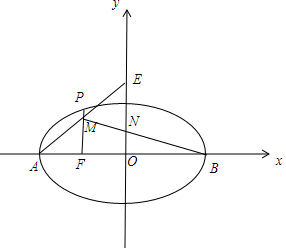
令x=-c,代入椭圆方程可得y=±b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$=±$\frac{{b}^{2}}{a}$,
可得P(-c,±$\frac{{b}^{2}}{a}$),
设直线AE的方程为y=k(x+a),
令x=-c,可得M(-c,k(a-c)),令x=0,可得E(0,ka),
∵直线BM与y轴交于点N,NE=2ON,
∴N(0,$\frac{ka}{3}$),
由B,N,M三点共线,可得kBN=kBM,
即为$\frac{\frac{ka}{3}}{-a}$=$\frac{k(a-c)}{-c-a}$,
化简可得$\frac{a-c}{a+c}$=$\frac{1}{3}$,即为a=2c,
可得e=$\frac{c}{a}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的方程和性质,以及直线方程的运用和三点共线的条件:斜率相等,考查化简整理的运算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.设函数f(x)=t|x-t|(t≠0)在区间(-∞,-1]上单调递增,则t的取值范围是( )
| A. | (-∞,-1] | B. | [-1,0) | C. | (0,1] | D. | [1,+∞) |
6.若点P(x0,y0)是曲线y=xex上任意一点,则|x0-y0-4|的最小值为( )
| A. | 4 | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2 |
13.将正方形ABCD沿对角线AC折起成直二面角,则直线BD和平面ABC所成的角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,则下列结论:
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,则下列结论: