题目内容
△ABC中,AB边的高为CD,若 ,
, ,
, ,|
,| |=1,|
|=1,| |=2,则
|=2,则
- A.

- B.

- C.

- D.

D
分析:根据射影定理可求出AD的长,从而得到向量 与向量
与向量 的关系,从而可求出向量
的关系,从而可求出向量 .
.
解答:∵
∴ 即AC⊥BC
即AC⊥BC
而AB边的高为CD, ,
, ,|
,| |=1,|
|=1,| |=2
|=2
根据射影定理可知AC2=AD×AB即4=AD× 即AD=
即AD=
而AB=
∴ =
=
故选D.
点评:本题主要考查了平面向量的数量积,以及射影定理的运用,同时考查了运算求解的能力,属于基础题.
分析:根据射影定理可求出AD的长,从而得到向量
 与向量
与向量 的关系,从而可求出向量
的关系,从而可求出向量 .
.解答:∵

∴
 即AC⊥BC
即AC⊥BC而AB边的高为CD,
 ,
, ,|
,| |=1,|
|=1,| |=2
|=2根据射影定理可知AC2=AD×AB即4=AD×
 即AD=
即AD=
而AB=

∴
 =
=
故选D.
点评:本题主要考查了平面向量的数量积,以及射影定理的运用,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
 =
= ,
, =
= ,
, •
• =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )
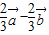
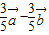

 =
= ,
,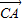 =
= ,
, •
• =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )
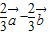


 =
= ,
, =
= ,
, •
•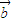 =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )


