题目内容
△ABC中,AB边的高为CD,若
=
,
=
,
•
=0,|
|=1,|
|=2,则
=
-
-
.
| CB |
| a |
| CA |
| b |
| a |
| b |
| a |
| b |
| AD |
| 4 |
| 5 |
| a |
| 4 |
| 5 |
| b |
| 4 |
| 5 |
| a |
| 4 |
| 5 |
| b |
分析:由已知,先容易得出∠C为直角,利用勾股定理得出AB,AD长,利用向量共线定理得出
=
=
(
-
)=
-
| AD |
| 4 |
| 5 |
| AB |
| 4 |
| 5 |
| a |
| b |
| 4 |
| 5 |
| a |
| 4 |
| 5 |
| b |
解答: 解:由已知,∠C为直角,如图所示:
解:由已知,∠C为直角,如图所示:
由勾股定理得出AB=
,CD=
=
所以在RT△BDC中,利用勾股定理求出AD=
所以
=
=
(
-
)=
-
故答案为:
-
 解:由已知,∠C为直角,如图所示:
解:由已知,∠C为直角,如图所示:由勾股定理得出AB=
| 5 |
| 1×2 | ||
|
| 2 | ||
|
所以在RT△BDC中,利用勾股定理求出AD=
| 4 | ||
|
所以
| AD |
| 4 |
| 5 |
| AB |
| 4 |
| 5 |
| a |
| b |
| 4 |
| 5 |
| a |
| 4 |
| 5 |
| b |
故答案为:
| 4 |
| 5 |
| a |
| 4 |
| 5 |
| b |
点评:本题考查平面向量基本定理及其意义,考查了向量共线定理,向量减法的几何意义.考查数形结合的思想,转化的能力.

练习册系列答案
相关题目
 =
= ,
, =
= ,
, •
• =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )
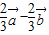
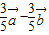

 =
= ,
,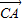 =
= ,
, •
• =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )
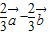


 =
= ,
, =
= ,
, •
•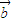 =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )


