题目内容
△ABC中,AB边的高为CD,若
=
,
=
,
•
=0,|
|=1,|
|=2,则
=( )
| CB |
| a |
| CA |
| b |
| a |
| b |
| a |
| b |
| AD |
分析:由题意可得,CA⊥CB,CD⊥AB,由摄影定理可得,AC2=AD•AB可求AD,进而可求
,从而可求
与
的关系,进而可求
| AD |
| AB |
| AD |
| AB |
解答: 解:∵
解:∵
•
=0,
∴CA⊥CB
∵CD⊥AB
∵|
|=1,|
|=2
∴AB=
由射影定理可得,AC2=AD•AB
∴AD=
=
∴
=
=
∴
=
=
(
-
)=
(
-
)
故选D
 解:∵
解:∵| a |
| b |
∴CA⊥CB
∵CD⊥AB
∵|
| a |
| b |
∴AB=
| 5 |
由射影定理可得,AC2=AD•AB
∴AD=
| 4 | ||
|
4
| ||
| 5 |
∴
| AD |
| AB |
| ||||
|
| 4 |
| 5 |
∴
| AD |
| 4 |
| 5 |
| AB |
| 4 |
| 5 |
| CB |
| CA |
| 4 |
| 5 |
| a |
| b |
故选D
点评:本题主要考查了直角三角形的摄影定理的应用,向量的基本运算的应用,向量的数量积的性质的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =
= ,
, =
= ,
, •
• =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )
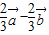
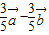

 =
= ,
,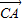 =
= ,
, •
• =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )
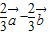


 =
= ,
, =
= ,
, •
•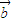 =0,|
=0,| |=1,|
|=1,| |=2,则
|=2,则 =( )
=( )


