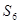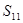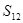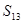题目内容
已知无穷数列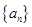 中,
中,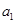 、
、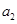 、
、 、
、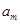 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,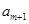 、
、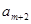 、
、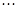 、
、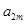 ,构成首项为
,构成首项为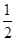 ,公比为
,公比为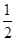 的等比数列,其中
的等比数列,其中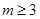 ,
,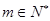 .
.
(1)当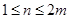 ,
,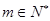 ,时,求数列
,时,求数列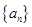 的通项公式;
的通项公式;
(2)若对任意的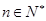 ,都有
,都有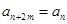 成立.
成立.
①当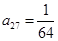 时,求
时,求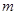 的值;
的值;
②记数列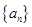 的前
的前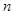 项和为
项和为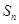 .判断是否存在
.判断是否存在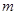 ,使得
,使得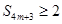 成立?若存在,求出
成立?若存在,求出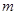 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
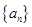 中,
中,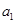 、
、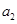 、
、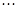 、
、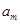 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,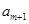 、
、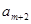 、
、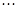 、
、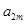 ,构成首项为
,构成首项为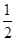 ,公比为
,公比为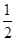 的等比数列,其中
的等比数列,其中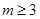 ,
,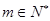 .
.(1)当
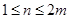 ,
,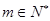 ,时,求数列
,时,求数列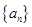 的通项公式;
的通项公式;(2)若对任意的
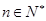 ,都有
,都有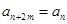 成立.
成立.①当
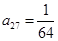 时,求
时,求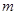 的值;
的值;②记数列
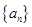 的前
的前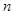 项和为
项和为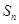 .判断是否存在
.判断是否存在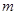 ,使得
,使得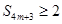 成立?若存在,求出
成立?若存在,求出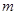 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)数列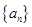 的通项公式为
的通项公式为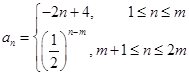 ;
;
(2)①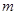 的值为
的值为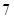 或
或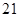 ;②详见解析.
;②详见解析.
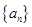 的通项公式为
的通项公式为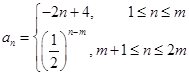 ;
;(2)①
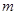 的值为
的值为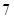 或
或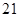 ;②详见解析.
;②详见解析.试题分析:(1)根据数列的定义求出当
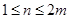 时数列
时数列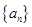 的通项公式,注意根据
的通项公式,注意根据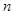 的取值利用分段数列的形式表示数列
的取值利用分段数列的形式表示数列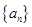 的通项;(2)①先确定
的通项;(2)①先确定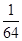 是等差数列部分还是等比数列部分中的项,然后根据相应的通项公式以及数列的周期性求出
是等差数列部分还是等比数列部分中的项,然后根据相应的通项公式以及数列的周期性求出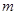 的值;②在(1)的基础上,先将数列
的值;②在(1)的基础上,先将数列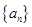 的前
的前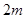 项和求出,然后利用周期性即可求出
项和求出,然后利用周期性即可求出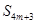 ,构造
,构造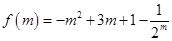 ,利用定义法求出
,利用定义法求出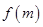 的最大值,从而确定
的最大值,从而确定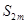 和
和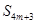 的最大值,进而可以确定是否存在
的最大值,进而可以确定是否存在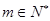 ,使得
,使得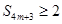 .
.试题解析:(1)当
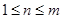 时,由题意得
时,由题意得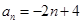 , 2分
, 2分当
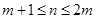 时,由题意得
时,由题意得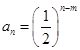 , 4分
, 4分故数列
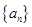 的通项公式为
的通项公式为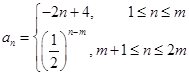 5分
5分(2)①因为
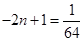 无解,所以
无解,所以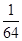 必不在等差数列内,
必不在等差数列内,因为
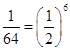 ,所以
,所以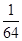 必在等比数列内,且等比数列部分至少有
必在等比数列内,且等比数列部分至少有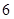 项,
项,则数列的一个周期至少有
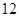 项, 7分
项, 7分所以第
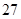 项只可能在数列的第一个周期或第二个周期内,
项只可能在数列的第一个周期或第二个周期内,若
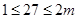 时,则
时,则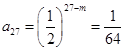 ,得
,得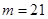 ,
,若
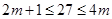 ,则
,则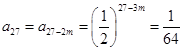 ,得
,得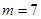 ,
,故
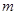 的值为
的值为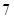 或
或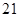 9分
9分②因为
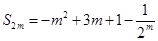 ,
,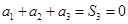 ,
,所以
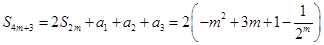 , 12分
, 12分记
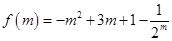 ,则
,则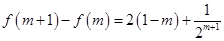 ,
,因为
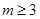 ,所以
,所以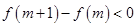 ,即
,即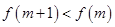 , 14分
, 14分故
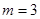 时,
时,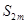 取最大,最大值为
取最大,最大值为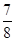 ,
,从而
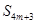 的最大值为
的最大值为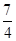 ,不可能有
,不可能有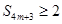 成立,故不存在满足条件的实数
成立,故不存在满足条件的实数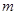 16分
16分 项和、数列的周期性、数列的单调性
项和、数列的周期性、数列的单调性
练习册系列答案
相关题目
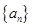 的前三项依次为
的前三项依次为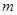 、4、
、4、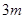 ,前
,前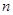 项和为
项和为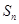 ,且
,且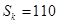 .
.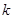 的值;
的值;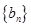 的通项
的通项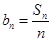 ,证明数列
,证明数列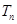 .
.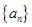 的前
的前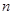 项和
项和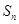 ,且
,且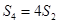 ,
,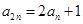 .
.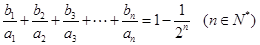 ,求数列
,求数列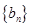 的前
的前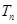 .
.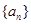 满足:
满足: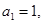


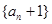 为等比数列,并求出数列
为等比数列,并求出数列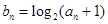 ,求数列
,求数列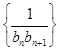 的前
的前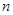 项和
项和 .
. 的前
的前 项和为
项和为 ,且
,且 则
则 ( )
( ) 是等差数列,
是等差数列, ,其中
,其中 ,则此数列的前
,则此数列的前 项和
项和 _______ .
_______ . 的前
的前 项和为
项和为 ,已知
,已知 .
. ;
; 求
求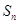 为等差数列
为等差数列 的前
的前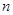 项和,
项和,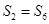 ,
,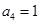 ,正项等比数列
,正项等比数列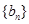 中,
中,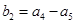 ,
,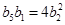 ,则
,则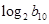 =( )
=( )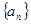 的前
的前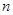 项之和为
项之和为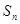 ,若
,若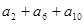 为一个确定的常数,则下列各数中也可以确定的是( )
为一个确定的常数,则下列各数中也可以确定的是( )