Question

已知函数f（x）=

1

3

x³+（1-b）x²-a（b-3）x+b-2的图象过原点，且在原点处的切线斜率是-3，则不等式组

x-ay≥0 x-by≥0

所确定的平面区域在x²+y²=4内的面积为（　　）

• A、

  π

  3

• B、

  π

  2

• C、π
• D、2π

Answer 1

考点：二元一次不等式（组）与平面区域,导数的几何意义

专题：导数的综合应用,不等式的解法及应用

分析：根据条件求出a，b的值以及函数f（x）的表达式，结合二元一次不等式（组）与平面区域的关系画出其表示的平面区域，再利用圆的方程画出图形，最后利用扇形面积公式计算即可．

解答： 解：因为函数f（x）的图象过原点，所以f（0）=0，即b=2．
则f（x）=

1

3

x³-x²+ax，
函数的导数f′（x）=x²-2x+a，
因为原点处的切线斜率是-3，
即f′（0）=-3，
所以f′（0）=a=-3，
故a=-3，b=2，
所以不等式组

x-ay≥0 x-by≥0

为

x+3y≥0 x-2y≥0

则不等式组

x+3y≥0 x-2y≥0

确定的平面区域在圆x²+y²=4内的面积，
如图阴影部分表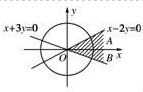示，
所以圆内的阴影部分扇形即为所求．
∵k_OB=-

1

3

，k_OA=

1

2

，
∴tan∠BOA=

1 2 -(- 1 3 )

1+ 1 2 ×(- 1 3 )

=

5 6

5 6

=1，
∴∠BOA=

π

4

，
∴扇形的圆心角为

π

4

，扇形的面积是圆的面积的八分之一，
∴圆x²+y²=4在区域D内的面积为

1

8

×4×π=

π

2

，
故选：B

点评：本题主要考查导数的应用，以及线性规划的应用，根据条件求出参数a，b的是值，然后借助不等式区域求解面积是解决本题的关键．