题目内容
4.在半径为r的圆中,扇形的周长等于半圆的弧长,那么扇形的圆心角是多少弧度?扇形的面积是多少?分析 设出扇形的圆心角,利用弧长公式得到弧长,代入题中条件,求出圆心角的弧度数,利用扇形的面积公式求扇形的面积.
解答 解:设扇形的圆心角是θrad,因为扇形的弧长是rθ,
所以扇形的周长是2r+rθ.
依题意得2r+rθ=πr,
解得θ=π-2,
所以扇形的面积为:
S=$\frac{1}{2}$r2θ=$\frac{1}{2}$(π-2)r2.
点评 本题考查了扇形的圆心角,弧长公式以及扇形的面积公式的应用问题,是基础题目.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
19.在△ABC中,若acosB=bcosA,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
16.已知f(x)=$\left\{\begin{array}{l}{x^2,-1≤x≤0}\\{1,0<x≤1}\end{array}\right.$则${∫}_{-1}^{1}$f(x)dx的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
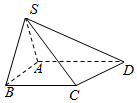 如图:在四棱锥S-ABCD中,已知∠DAB=∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=a,AD=2a,求直线SD与AC所成的角的大小.
如图:在四棱锥S-ABCD中,已知∠DAB=∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=a,AD=2a,求直线SD与AC所成的角的大小.