题目内容
某公司生产甲、乙两种桶装产品．已知生产甲产品1桶需耗A原料1 kg、B原料2 kg；生产乙产品1桶需耗A原料2 kg，B原料1 kg.每桶甲产品的利润是300元，每桶乙产品的利润是400元．公司在生产这两种产品的计划中，要求每天消耗A、B原料都不超过12 kg.通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是多少？
解：设公司每天生产甲种产品x桶，乙种产品y桶，公司共可获得利润为z元/天，则由已知，得z＝300x＋400y，
且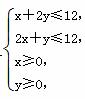
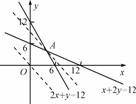
画可行域如图所示，
目标函数z＝300x＋400y可变形为y＝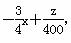
，
这是随z变化的一簇平行直线，
解方程组
即A(4，4)，
∴ zmax＝1 200＋1 600＝2 800(元)．
故公司每天生产甲产品4桶、生产乙产品4桶时，可获得最大利润为2 800元．
练习册系列答案
相关题目
，则直线的斜率为（ ）
B．
C．
D．
所表示的平面区域被直线y＝kx＋
分为面积相等的两部分，则k＝________．某农户计划种植黄瓜和韭菜，种植面积不超过50亩，投入资金不超过54万元，假设种植黄瓜和韭菜的产量、成本和售价如下表：
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4 t | 1.2万元 | 0.55万元 |
| 韭菜 | 6 t | 0.9万元 | 0.3万元 |
为使一年的种植的总利润最大，那么黄瓜和韭菜的种植面积分别为________．
%，第二次提价
的最小值为________．