题目内容
函数f(x)=x2+ax+3.
(1) 当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2) 当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
解:(1) ∵ x∈R,f(x)≥a恒成立,
∴ x2+ax+3-a≥0恒成立,
则Δ=a2-4(3-a)≤0,得-6≤a≤2.
∴ 当x∈R时,f(x)≥a恒成立,则a的取值范围为[-6,2].
(2) f(x)=
讨论对称轴与[-2,2]的位置关系,得到a的取值满足下列条件:
 解得-7≤a≤2.∴ 当x∈[-2,2]时,f(x)≥a恒成立,则a的取值范围为[-7,2].
解得-7≤a≤2.∴ 当x∈[-2,2]时,f(x)≥a恒成立,则a的取值范围为[-7,2].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则角
,则角 所在的象限是
所在的象限是  <b,且f (x)=
<b,且f (x)=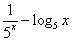 ,则下列大小关系式成立的是( ).
,则下列大小关系式成立的是( ).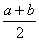 )<f (
)<f (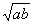 ) B、f (
) B、f ( <1.
<1. ,则f(10x)>0的解集为______.
,则f(10x)>0的解集为______. 则z=2x+y的最小值是________.
则z=2x+y的最小值是________.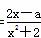 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.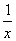 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围. 的值.
的值.