题目内容
函数y=Asin（ωx+?）（x∈R，A＞0，ω＞0，|?|＜
）的图象上相邻的最高点与最低点的坐标分别为M（
），N（
，-3），
（1）求此函数的解析式；
（2）写出函数的单调区间．
解：（1）由题意知，
，且A=3
∴T=π∴
∴函数y=3sin（2x+?）
把
，y=3代入上式得，
∴
，k∈Z，
解得：
，k∈Z，
又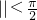
∴
∴函数解析式是
，x∈R．
（2）因为
，k∈Z，
所以
，k∈Z，
因为
，k∈Z，
所以
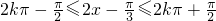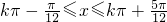，k∈Z，
所以函数的单调增区间为：
，k∈Z，
调减区间为：
，k∈Z．
分析：（1）利用题目中图象上相邻的最高点与最低点的坐标求出函数的周期，与A，求出ω，利用最高点的坐标分别为M（
，求出?，得到函数的解析式；
（2）利用正弦函数的单调性，求出函数的单调区间．
点评：本题是中档题，考查三角函数的解析式的求法，函数的单调区间的求法，考查计算能力．
，且A=3∴T=π∴
∴函数y=3sin（2x+?）
把
，y=3代入上式得，∴
，k∈Z，解得：
，k∈Z，又
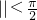∴∴函数解析式是
，x∈R．（2）因为
，k∈Z，所以
，k∈Z，因为
，k∈Z，所以
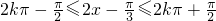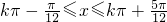，k∈Z，所以函数的单调增区间为：
，k∈Z，调减区间为：
，k∈Z．分析：（1）利用题目中图象上相邻的最高点与最低点的坐标求出函数的周期，与A，求出ω，利用最高点的坐标分别为M（
，求出?，得到函数的解析式；（2）利用正弦函数的单调性，求出函数的单调区间．
点评：本题是中档题，考查三角函数的解析式的求法，函数的单调区间的求法，考查计算能力．
练习册系列答案
相关题目
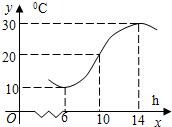如图所示，某地一天从6时到14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，则8时的温度大约为
如图，是函数y=Asin（ωx+φ），（-π＜φ＜π）的图象的一段，O是坐标原点，P是图象的最高点，A点坐标为（5，0），若