题目内容
已知圆心为C的圆经过点A(0,-6),B(1,-5),且圆心在直线l:x-y+1=0上,求圆的标准方程
【解】(1)法一:设圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
则圆心坐标为
消去F得 代入求得F=-12,
代入求得F=-12,
所以圆的方程为x2+y2+6x+4y-12=0,
标准方程为(x+3)2+(y+2)2=25.
法二:因为A(0,-6),B(1,-5),所以线段AB的中点D的坐标为 ,
,
直线AB的斜率kAB= =1,因此线段AB的垂直平分线l的方程是
=1,因此线段AB的垂直平分线l的方程是


练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 与
与 的交点,且与直线
的交点,且与直线 平行的直线方程.
平行的直线方程. 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切,则圆
相切,则圆 两点,圆心在
两点,圆心在 轴上,则圆
轴上,则圆 B.
B. C.
C. D.
D.
 向圆
向圆 :
: 所引的切线方程.
所引的切线方程.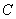 :
: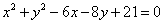 和直线
和直线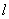 :
: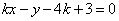 .
.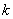 取何值时直线
取何值时直线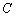 总相交;
总相交;