题目内容
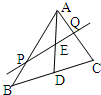
过△ABC的中线AD的中点E作直线PQ分别交AB、AC于P、Q两点，若
=m
，
=n
，则
+
=（ ）
| AP |
| AB |
| AQ |
| AC |
| 1 |
| m |
| 1 |
| n |
分析：由D为BC的中点可知，
=
+
=
(
+
)，
=
(
+
)=
m
+
n
及
=
，结合
与
不共线可得关于m，n的方程，从而可求m，n，进而可求
| AD |
| AB |
| BD |
| 1 |
| 2 |
| AB |
| AC |
| AE |
| 1 |
| 2 |
| AP |
| AQ |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| AE |
| 1 |
| 2 |
| AD |
| AB |
| AC |
解答：解：由D为BC的中点可知，
=
+
=
+
=
+
(
-
)
=
(
+
)
∵
=m
，
=n
，
∴
=
(
+
)=
m
+
n
∵
=
∴
m
+
n
=
∴(
m-
)
=(
-
n)
∵
与
不共线
∴
m-
=0，
-
n=0
∴m=n=
，
+
=4
故选A
| AD |
| AB |
| BD |
| AB |
| 1 |
| 2 |
| BC |
| AB |
| 1 |
| 2 |
| AC |
| AB |
=
| 1 |
| 2 |
| AB |
| AC |
∵
| AP |
| AB |
| AQ |
| AC |
∴
| AE |
| 1 |
| 2 |
| AP |
| AQ |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
∵
| AE |
| 1 |
| 2 |
| AD |
∴
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| ||||
| 4 |
∴(
| 1 |
| 2 |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| 1 |
| 2 |
| AC |
∵
| AB |
| AC |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴m=n=
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| n |
故选A
点评：本题主要考查了向量的基本运算的应用，向量的基本定理的应用及向量共线定理等知识的综合应用．
练习册系列答案
相关题目
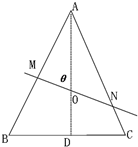如图点O是边长为1的等边三角形ABC的边BC中线AD上一点，且|AO|=2|OD|，过O的直线交边AB于M，交边AC于N，记∠AOM=θ，
＝x
，
＝y
记y＝f(x)
＝x
，
＝y
，记y＝f(x)
，1]，总存在x2∈[0，1]使得f(x1)＝g(x2)成立，求实数a的取值范围；
，则
=
