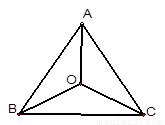题目内容
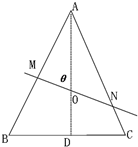如图点O是边长为1的等边三角形ABC的边BC中线AD上一点，且|AO|=2|OD|，过O的直线交边AB于M，交边AC于N，记∠AOM=θ，（1）则θ的取值范围为
[
，
]
| π |
| 3 |
| 2π |
| 3 |
[
，
]
| π |
| 3 |
| 2π |
| 3 |
（2）
| 1 |
| |OM|2 |
| 1 |
| |ON|2 |
15
15
．分析：（1）由题意可得，点O为等边三角形ABC的重心，当点N与点C重合时，θ最小，由cosθ=
，可得θ的值．当M与B重合时，θ取得最大值，由于cos（π-θ）=
，可得θ的值，从而求得θ的取值范围．
（2）先求得AO=
AD的值，设∠ANO=α，则∠AMO=
-α．△ANO中，由正弦定理求得 ON=
，同理求得 OM=
，计算
+
=12+6cos（2α+
）．由
≤
-（
-α）≤
，求得α的范围，利用余弦函数的定义域和值域求得12+6cos（2α+
） 的最小值．
| MO |
| AO |
| ON |
| AO |
（2）先求得AO=
| 2 |
| 3 |
| 2π |
| 3 |
| ||
| 6sinα |
| ||
6Sin(
|
| 1 |
| |OM|2 |
| 1 |
| |ON|2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
解答：解：（1）由题意可得，点O为等边三角形ABC的重心，
当点N与点C重合时，MN与AB垂直，M为AB的中点，OM取得最小值，
此时，θ最小，由cosθ=
=
，可得θ=
．
当M与B重合时，此时，MN垂直于AC，θ取得最大值，由于cos（π-θ）=
=
，可得θ=
．
综上可得，θ的取值范围为[
，
]．
（2）由题意可得，AO=
AD=
×
=
；设∠ANO=α，则∠AMO=
-α．
△ANO中，由余弦定理可得
=
，解得 ON=
．
同理求得 OM=
．
∴
+
=
+
=12×
+12×
=12-6[cos（
-2α）+cos2α]
=12+6cos（2α+
）．
由（1）可得
≤
-（
-α）≤
，可得
≤2α≤π，
∴
≤2α+
≤π+
，
-1≤cos（2α+
）≤-
，故当2α+
=π 时，cos（2α+
） 取得最小值为-1，
12+6cos（2α+
） 取得最小值为 12-6=6，
故答案为 6．
当点N与点C重合时，MN与AB垂直，M为AB的中点，OM取得最小值，
此时，θ最小，由cosθ=
| MO |
| AO |
| 1 |
| 2 |
| π |
| 3 |
当M与B重合时，此时，MN垂直于AC，θ取得最大值，由于cos（π-θ）=
| ON |
| AO |
| 1 |
| 2 |
| 2π |
| 3 |
综上可得，θ的取值范围为[
| π |
| 3 |
| 2π |
| 3 |
（2）由题意可得，AO=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| 2π |
| 3 |
△ANO中，由余弦定理可得
| ON |
| sin30° |
| AO |
| sinα |
| ||
| 6sinα |
同理求得 OM=
| ||
6Sin(
|
∴
| 1 |
| |OM|2 |
| 1 |
| |ON|2 |
36sin2(
| ||
| 3 |
| 36sin2α |
| 3 |
=12×
1-cos(
| ||
| 2 |
| 1-cos2α |
| 2 |
| 4π |
| 3 |
=12+6cos（2α+
| π |
| 3 |
由（1）可得
| π |
| 3 |
| 5π |
| 6 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
∴
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
-1≤cos（2α+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
12+6cos（2α+
| π |
| 3 |
故答案为 6．
点评：本题主要考查正弦定理、余弦定理的应用，余弦函数的定义域和值域，属于难题．
练习册系列答案
相关题目
如图，已知点O是边长为1的等边△ABC的中心，则（
，过O的直线交边AB于M，交边AC于N，记∠AOM=
，
的最小值为________.
)·(
)等于
B．
C．
D．
)·(
)等于
B．
C．
D．
