题目内容
设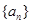 是公比
是公比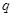 大于1的等比数列,
大于1的等比数列,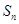 为数列
为数列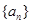 的前
的前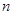 项和,已知
项和,已知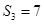 ,且
,且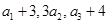 构成等差数列.
构成等差数列.
(1)求数列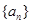 的通项公式;
的通项公式;
(2)令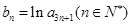 ,求数列
,求数列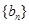 的前
的前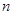 项和
项和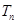 .
.
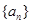 是公比
是公比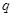 大于1的等比数列,
大于1的等比数列,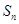 为数列
为数列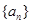 的前
的前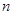 项和,已知
项和,已知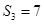 ,且
,且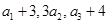 构成等差数列.
构成等差数列.(1)求数列
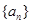 的通项公式;
的通项公式;(2)令
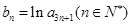 ,求数列
,求数列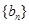 的前
的前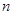 项和
项和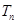 .
.(1) (2)
(2)
 (2)
(2)
试题分析:(1)由已知得
 ,即
,即 ,结合
,结合 解得
解得 ∴
∴ 
(2)由(1)得,
 ,∴
,∴ ,∴
,∴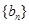 是以
是以 为首项,公差
为首项,公差 的等差数列,∴
的等差数列,∴
即

点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
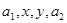 成等差数列,
成等差数列, 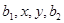 成等比数列.则
成等比数列.则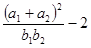 的取值范围是( )
的取值范围是( )



 的前n项和为
的前n项和为 ,若
,若 ,则当
,则当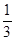 )是函数
)是函数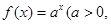 且
且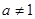 )的图象上一点,等比数列
)的图象上一点,等比数列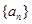 的前
的前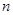 项和为
项和为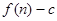 ,数列
,数列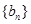
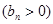 的首项为
的首项为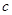 ,且前
,且前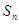 满足
满足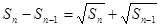 (
(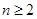 ).
).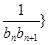 前
前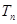 ,问
,问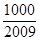 的最小正整数
的最小正整数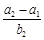 的值是( ).
的值是( ).

 中,
中, ,不等式
,不等式
 对任意
对任意 都成立.
都成立. 的取值范围;
的取值范围; ,
, ,求证:对任意的
,求证:对任意的 .
.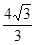 tan x+1=0在x
tan x+1=0在x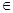 [0,n
[0,n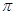 )( n
)( n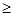 bn,求实数k的取值范围.
bn,求实数k的取值范围. 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 .
. 及
及 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 是等差数列,数列
是等差数列,数列 是等比数列,则
是等比数列,则 的值为 .
的值为 .