题目内容
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.

(1)求证:EF⊥BC;
(2)求二面角E BF
BF C的正弦值.
C的正弦值.
(1)证明:法一 过E作EO⊥BC,垂足为O,连OF.
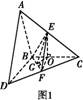
由△ABC≌△DBC可证出△EOC≌△FOC.
所以∠EOC=∠FOC= ,
,
即FO⊥BC.
又EO⊥BC,
因此BC⊥平面EFO,
又EF⊂平面EFO,
所以EF⊥BC.
法二 由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图2所示空间直角坐标系.
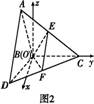
易得B(0,0,0),A(0,-1,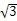 ),
),
D(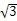 ,-1,0),C(0,2,0).
,-1,0),C(0,2,0).
因而E(0, ,
,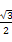 ),F(
),F(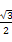 ,
, ,0),
,0),
所以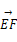 =(
=(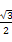 ,0,-
,0,-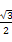 ),
),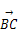 =(0,2,0),
=(0,2,0),
因此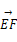 ·
·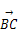 =0.
=0.
从而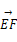 ⊥
⊥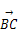 ,
,
所以EF⊥BC.
(2)解:法一 在图1中,过O作OG⊥BF,垂足为G,连EG.
由平面ABC⊥平面BDC,
从而EO⊥平面BDC,
又OG⊥BF,
由三垂线定理知EG⊥BF.
因此∠EGO为二面角E BF
BF C的平面角.
C的平面角.
在△EOC中,EO= EC=
EC= BC·cos 30°=
BC·cos 30°=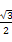 ,
,
由△BGO∽△BFC知,OG=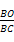 ·FC=
·FC=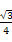 ,
,
因此tan∠EGO=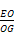 =2,
=2,
从而sin∠EGO=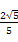 ,
,
即二面角E BF
BF C的正弦值为
C的正弦值为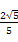 .
.
法二 在图2中,平面BFC的一个法向量为n1=(0,0,1).
设平面BEF的法向量为n2=(x,y,z),
又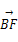 =(
=(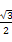 ,
, ,0),
,0),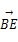 =(0,
=(0, ,
,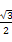 ).
).
由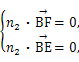
得其中一个n2=(1,-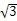 ,1).
,1).
设二面角E BF
BF C的大小为θ,
C的大小为θ,
且由题意知θ为锐角,
则cos θ=|cos<n1,n2>=|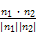 |=
|=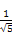 ,
,
因此sin θ=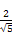 =
=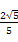 ,
,
即所求二面角的正弦值为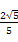 .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.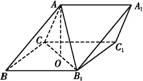


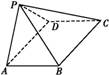
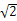 ,PC=2,问AB为何值时,四棱锥P
,PC=2,问AB为何值时,四棱锥P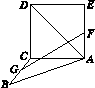
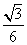 B.-
B.-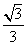 D.-
D.-