题目内容
(本题满分13分) 已知函数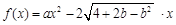 ,
,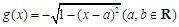 .
.
(1)当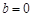 时,若
时,若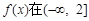 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对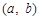 :存在
:存在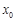 ,使得
,使得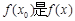 的最大值,
的最大值,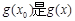 的最小值;
的最小值;
【答案】
(1)当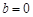 时,
时,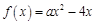 , ………………………………………1分
, ………………………………………1分
若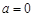 ,
,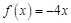 ,则
,则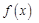 在
在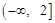 上单调递减,符合题意;………3分
上单调递减,符合题意;………3分
若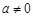 ,要使
,要使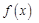 在
在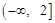 上单调递减,
上单调递减,
必须满足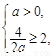 ……………………………………………………5分
……………………………………………………5分
∴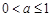 .综上所述,a的取值范围是
.综上所述,a的取值范围是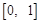 …………………………………6分
…………………………………6分
(2)若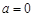 ,
,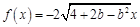 ,则
,则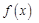 无最大值, 故
无最大值, 故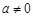 ,∴
,∴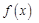 为二次函数,
为二次函数,
要使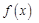 有最大值,必须满足
有最大值,必须满足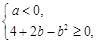
即 且
且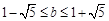 ,
…………………………………………8分
,
…………………………………………8分
此时,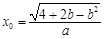 时,
时,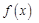 有最大值. ………………………………………9分
有最大值. ………………………………………9分
又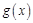 取最小值时,
取最小值时,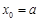 , ………………………………………………………10分
, ………………………………………………………10分
依题意,有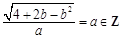 ,则
,则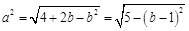 , …………11分
, …………11分
∵ 且
且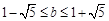 ,∴
,∴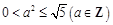 ,得
,得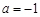 , ………………12分
, ………………12分
此时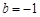 或
或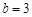 .
.
∴满足条件的整数对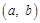 是
是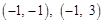 . …………………………13分
. …………………………13分
【解析】略

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.