题目内容
(2014·哈尔滨模拟)已知函数f(x)=x2+ ,g(x)=
,g(x)=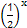 -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
 ,g(x)=
,g(x)=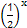 -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.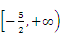
要使?x1∈[1,2],?x2∈[-1,1],
使f(x1)≥g(x2),只需f(x)=x2+ 在[1,2]上的最小值大于等于g(x)=
在[1,2]上的最小值大于等于g(x)=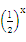 -m在[-1,1]上的最小值,
-m在[-1,1]上的最小值,
因为f′(x)=2x- =
=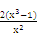 ≥0在[1,2]上成立,且f′(1)=0,
≥0在[1,2]上成立,且f′(1)=0,
所以f(x)=x2+ 在[1,2]上单调递增,
在[1,2]上单调递增,
所以f(x)min=f(1)=12+ =3.
=3.
因为g(x)=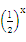 -m是单调递减函数,
-m是单调递减函数,
所以g(x)min=g(1)= -m,
-m,
所以 -m≤3,即m≥-
-m≤3,即m≥- .
.
使f(x1)≥g(x2),只需f(x)=x2+
 在[1,2]上的最小值大于等于g(x)=
在[1,2]上的最小值大于等于g(x)=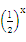 -m在[-1,1]上的最小值,
-m在[-1,1]上的最小值,因为f′(x)=2x-
 =
=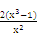 ≥0在[1,2]上成立,且f′(1)=0,
≥0在[1,2]上成立,且f′(1)=0,所以f(x)=x2+
 在[1,2]上单调递增,
在[1,2]上单调递增,所以f(x)min=f(1)=12+
 =3.
=3.因为g(x)=
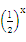 -m是单调递减函数,
-m是单调递减函数,所以g(x)min=g(1)=
 -m,
-m,所以
 -m≤3,即m≥-
-m≤3,即m≥- .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R. 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立; ,
, .
. 的极大值为
的极大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若
,若 关于实数a 可线性分解,求
关于实数a 可线性分解,求 取值范围.
取值范围.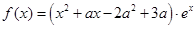 ,其中
,其中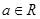 .
. ,使得函数
,使得函数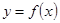 在
在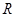 上单调递增?若存在,求出的
上单调递增?若存在,求出的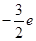 ,求函数的极大值。
,求函数的极大值。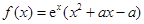 ,其中
,其中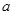 是常数.
是常数.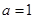 时,求曲线
时,求曲线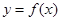 在点
在点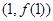 处的切线方程;
处的切线方程;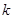 ,使得关于
,使得关于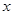 的方程
的方程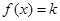 在
在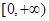 上有两个不相等的实数根,求
上有两个不相等的实数根,求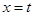 与函数
与函数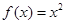 ,
,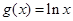 的图象分别交于M、N两点,则当MN达到最小时t的值为
的图象分别交于M、N两点,则当MN达到最小时t的值为