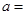题目内容
已知函数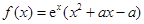 ,其中
,其中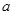 是常数.
是常数.
(1)当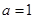 时,求曲线
时,求曲线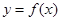 在点
在点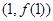 处的切线方程;
处的切线方程;
(2)若存在实数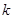 ,使得关于
,使得关于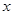 的方程
的方程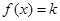 在
在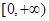 上有两个不相等的实数根,求
上有两个不相等的实数根,求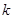 的取值范围.
的取值范围.
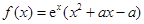 ,其中
,其中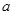 是常数.
是常数.(1)当
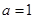 时,求曲线
时,求曲线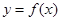 在点
在点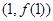 处的切线方程;
处的切线方程;(2)若存在实数
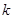 ,使得关于
,使得关于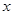 的方程
的方程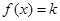 在
在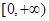 上有两个不相等的实数根,求
上有两个不相等的实数根,求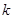 的取值范围.
的取值范围.(1)曲线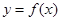 在点
在点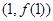 处的切线方程为
处的切线方程为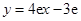
(2)要使方程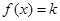 在
在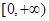 上有两个不相等的实数根,
上有两个不相等的实数根,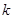 的取值范围必须是
的取值范围必须是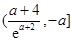 .
.
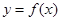 在点
在点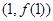 处的切线方程为
处的切线方程为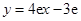
(2)要使方程
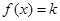 在
在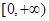 上有两个不相等的实数根,
上有两个不相等的实数根,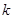 的取值范围必须是
的取值范围必须是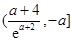 .
.解:(1)由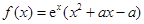 可得
可得
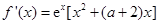 .
.
当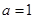 时,
时,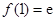 ,
,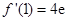 .
.
所以 曲线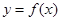 在点
在点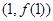 处的切线方程为
处的切线方程为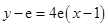 ,
,
即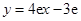 .
.
(2) 令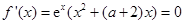 ,
,
解得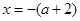 或
或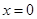 .
.
当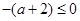 ,即
,即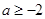 时,在区间
时,在区间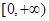 上,
上,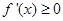 ,所以
,所以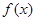 是
是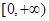 上的增函数.
上的增函数.
所以 方程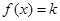 在
在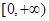 上不可能有两个不相等的实数根.
上不可能有两个不相等的实数根.
当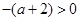 ,即
,即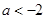 时,
时,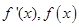 随
随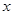 的变化情况如下表
的变化情况如下表
由上表可知函数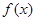 在
在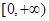 上的最小值为
上的最小值为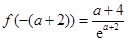 .
.
因为 函数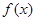 是
是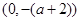 上的减函数,是
上的减函数,是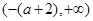 上的增函数,
上的增函数,
且当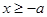 时,有
时,有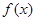
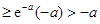 .
.
所以 要使方程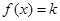 在
在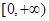 上有两个不相等的实数根,
上有两个不相等的实数根,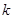 的取值范围必须是
的取值范围必须是
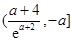 .
.
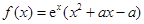 可得
可得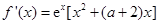 .
. 当
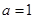 时,
时,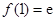 ,
,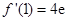 .
. 所以 曲线
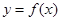 在点
在点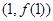 处的切线方程为
处的切线方程为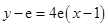 ,
,即
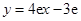 .
. (2) 令
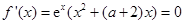 ,
,解得
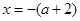 或
或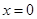 .
. 当
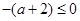 ,即
,即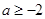 时,在区间
时,在区间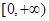 上,
上,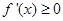 ,所以
,所以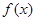 是
是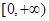 上的增函数.
上的增函数.所以 方程
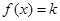 在
在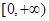 上不可能有两个不相等的实数根.
上不可能有两个不相等的实数根.当
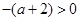 ,即
,即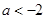 时,
时,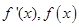 随
随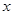 的变化情况如下表
的变化情况如下表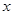 |  | 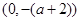 | 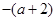 | 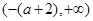 |
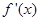 |  |  |  | 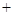 |
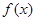 | 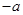 | ↘ | 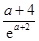 | ↗ |
由上表可知函数
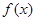 在
在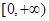 上的最小值为
上的最小值为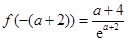 .
.因为 函数
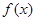 是
是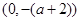 上的减函数,是
上的减函数,是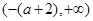 上的增函数,
上的增函数,且当
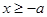 时,有
时,有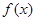
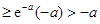 .
. 所以 要使方程
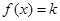 在
在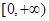 上有两个不相等的实数根,
上有两个不相等的实数根,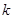 的取值范围必须是
的取值范围必须是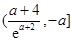 .
.
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 .
. 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程; ,且
,且 恒成立,求a的取值范围.
恒成立,求a的取值范围. 。
。 ,求
,求 的单调区间;
的单调区间; 时,
时, ,求a的取值范围。
,求a的取值范围。 时,函数
时,函数 的图象大致是
的图象大致是
 ,g(x)=
,g(x)=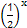 -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.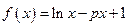
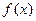 的极值点;
的极值点;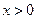 ,恒有
,恒有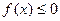 ,求
,求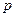 的取值范围.
的取值范围.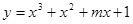 在实数集上是单调函数,则m的取值范围是 .
在实数集上是单调函数,则m的取值范围是 . ,其中
,其中 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;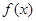 的单调区间及在
的单调区间及在 上的最大值.
上的最大值.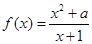 在
在 处取极值,则
处取极值,则