题目内容
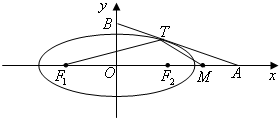
已知椭圆
+
=1,左焦点为F,右顶点为C,过F作直线l与椭圆交于A,B两点,求△ABC面积最大值.
| x2 |
| 4 |
| y2 |
| 3 |
由题意知:|FC|=a+c=2+1=3,F(-1,0),
设AB的直线方程x=my-1,不妨设直线AB与椭圆的交点A(x1,y1),B(x2,y2),
⇒(3m2+4)y2-6my-9=0,则y1+y2=
,y1y2=-
,
S△ABC=
×|FC|×|y1-y2|=
×3×
=18×
=18×
,
设t=m2+1≥1,函数g(t)=9t+
,g′(t)=9-
,∵t≥1,g′(t)>0
∴函数在[1,+∞)单调递增,
∴m2+1=1时,S△ABC最大,且最大值为
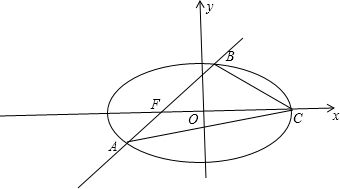
设AB的直线方程x=my-1,不妨设直线AB与椭圆的交点A(x1,y1),B(x2,y2),
|
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
|
|
设t=m2+1≥1,函数g(t)=9t+
| 1 |
| t |
| 1 |
| t2 |
∴函数在[1,+∞)单调递增,
∴m2+1=1时,S△ABC最大,且最大值为
| 9 |
| 2 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目