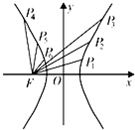
题目内容

过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）上任意一点P，作与实轴平行的直线，交两渐近线于M、N两点，若
PM
•
PN
=2b2，则该双曲线的离心率为（　　）
A．
6
3
B．
3
C．
6
2
D．
2
设双曲线上的P（x0，y0），则
x20
a2
-
y20
b2
=1，∴
x20
=a2+
a2
b2
y20
．
联立
y=y0
y=
b
a
x
，解得x=
ay0
b
，取M(
ay0
b
，y0)．
同理可得N(-
ay0
b
，y0)．
∴
PM
•
PN
=(
ay0
b
-x0，0)•(-
ay0
b
-x0，0)=
x20
-
a2
y20
b2
=a2．
∴a2=2b2．
∴e=
c
a
=
1+
b2
a2
=
1+
1
2
=
6
2
．
故选C．
练习册系列答案
相关题目
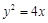已知抛物线的方程为，直线l过定点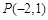，斜率为k．当k为何值时，直线l与该抛物线：只有一个公共点；有两个公共点；没有公共点？
双曲线
x2
4
-y2=1的一条渐近线方程为（　　）
A．y=
x
2
B．y=xC．y=2xD．y=4x
已知双曲线的两条渐近线方程为直线l1：y=
3
x和l2：y=-
3
x，其焦点在x轴上，实轴长为2．
（Ⅰ）求双曲线的方程；
（Ⅱ）设直线l：y=kx+1与双曲线相切于点M且与右准线交于N，F为右焦点，求证：∠MFN为直角．
若双曲线C与双曲线
x2
12
-
y2
8
=1共渐近线，且过点A(3，
2
)，则双曲线C的方程为______．
若方程
x2
k+2
+
y2
5-k
=-1表示双曲线，则k的取值范围是______．
如图所示，F为双曲线C：
x2
9
-
y2
16
=1的左焦点，双曲线C上的点Pi与P7-i（i=1，2，3）关于y轴对称，则|P1F|+|P2F|+|P3F|-|P4F|-|P5F|-|P6F|的值是______．
如图，点F2是⊙F1外的一点，点Q是⊙F1上的动点，射线F1Q交线段F2Q的中垂线于P，则点P一定在（　　）
A．以F1、F2为焦点，以2|F1Q|为长轴长的椭圆上
B．以F1、F2为焦点，以2|F1Q|为实轴长的双曲线上
C．以F2为焦点，以F1F2中点为顶点的抛物线上
D．以F1、F2为焦点，以|F1Q|为实轴长的双曲线上
双曲线
x2
4
-
y2
9
=-1的渐近线方程是（　　）
A．y=
+-
2
3
x		B．y=
+-
4
9
x		C．y=
+-
3
2
x		D．y=
+-
9
4
x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网