题目内容
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.(I)m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3. 的分布列为
的分布列为

所以E =2
=2
(II)
 的取值为0,1,2,3.
的取值为0,1,2,3. 的分布列为
的分布列为
所以E
 =2
=2第一问中利用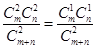 ,解得m=6,n=3.
,解得m=6,n=3.
第二问中, 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 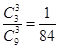 , P(
, P( =1)=
=1)= 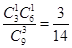
P( =2)=
=2)= 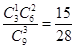 , P(
, P( =3)=
=3)= 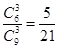
得到分布列和期望值
解:(I)据题意得到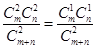 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3.
P( =0)=
=0)= 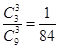 , P(
, P( =1)=
=1)= 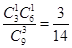
P( =2)=
=2)= 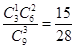 , P(
, P( =3)=
=3)= 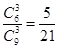
 的分布列为
的分布列为

所以E =2
=2
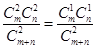 ,解得m=6,n=3.
,解得m=6,n=3.第二问中,
 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 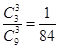 , P(
, P( =1)=
=1)= 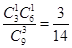
P(
 =2)=
=2)= 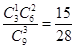 , P(
, P( =3)=
=3)= 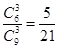
得到分布列和期望值
解:(I)据题意得到
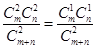 解得m=6,n=3.
解得m=6,n=3.(II)
 的取值为0,1,2,3.
的取值为0,1,2,3.P(
 =0)=
=0)= 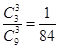 , P(
, P( =1)=
=1)= 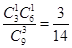
P(
 =2)=
=2)= 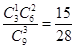 , P(
, P( =3)=
=3)= 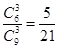
 的分布列为
的分布列为
所以E
 =2
=2
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
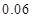
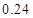
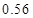
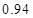
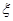 ,求
,求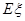 (即均值).
(即均值).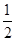 ,且相互独立,则灯泡亮的概率( )
,且相互独立,则灯泡亮的概率( )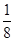 B.
B.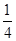 C.
C.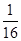
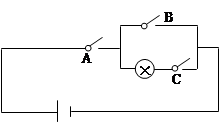
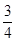 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是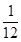 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是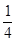 .(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用
.(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用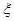 表示回答对该题的人数,求
表示回答对该题的人数,求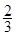 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.