题目内容
(10分)在一次国际大型体育运动会上,某运动员报名参加了其中5个项目的比赛.已知该运动员在这5个项目中,每个项目能打破世界纪录的概率都是0.8,那么在本次运动会上:
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为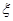 ,求
,求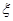 的数学期望
的数学期望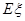 (即均值).
(即均值).
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为
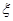 ,求
,求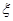 的数学期望
的数学期望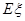 (即均值).
(即均值).(1) ;(2)4.
;(2)4.
 ;(2)4.
;(2)4.(1)利用互斥事件概率和公式及独立重复试验公式求解即可;(2)根据随机变量符合二项分布,故利用二项分布的数学期望公式求解出数学期望。
解:(Ⅰ)依题意,该运动员在每个项目上“能打破世界纪录”为独立事件,并且每个事件发生的概率相同. 设其打破世界纪录的项目数为随机变量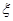 ,“该运动员至少能打破3项世界纪录”为事件A,则有
,“该运动员至少能打破3项世界纪录”为事件A,则有

 .
.
(Ⅱ)由(Ⅰ)解答可知,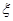 ~B(5,0.8),故所求数学期望为
~B(5,0.8),故所求数学期望为 .
.
解:(Ⅰ)依题意,该运动员在每个项目上“能打破世界纪录”为独立事件,并且每个事件发生的概率相同. 设其打破世界纪录的项目数为随机变量
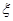 ,“该运动员至少能打破3项世界纪录”为事件A,则有
,“该运动员至少能打破3项世界纪录”为事件A,则有

 .
.(Ⅱ)由(Ⅰ)解答可知,
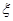 ~B(5,0.8),故所求数学期望为
~B(5,0.8),故所求数学期望为 .
. 
练习册系列答案
相关题目
 和
和 ,则两次射击中至少有一次命中目标的概率是( )
,则两次射击中至少有一次命中目标的概率是( )



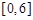 内任取两个数(可以相等),分别记为
内任取两个数(可以相等),分别记为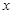 和
和 ,
,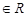 ,求
,求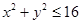 的概率.
的概率. ,求
,求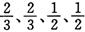 ,指标甲、乙、丙、丁被检测合格分别记4分、3分、2分、1分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
,指标甲、乙、丙、丁被检测合格分别记4分、3分、2分、1分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.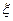 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.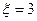 时的概率;
时的概率;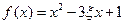 在区间
在区间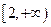 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率. 相互独立,若
相互独立,若 ,则
,则 .
.