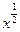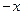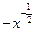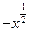题目内容
( 14分)已知函数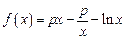 ,
,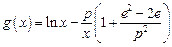 ,其中
,其中 为无理数
为无理数 .(1)若
.(1)若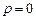 ,求证:
,求证: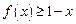 ;(2)若
;(2)若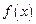 在其定义域内是单调函数,求
在其定义域内是单调函数,求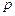 的取值范围;(3)对于区间(1,2)中的任意常数
的取值范围;(3)对于区间(1,2)中的任意常数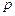 ,是否存在
,是否存在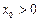 使
使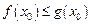 成立?
成立?
若存在,求出符合条件的一个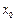 ;否则,说明理由.
;否则,说明理由.
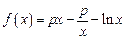 ,
,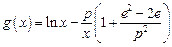 ,其中
,其中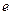 为无理数
为无理数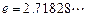 .(1)若
.(1)若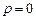 ,求证:
,求证: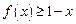 ;(2)若
;(2)若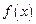 在其定义域内是单调函数,求
在其定义域内是单调函数,求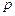 的取值范围;(3)对于区间(1,2)中的任意常数
的取值范围;(3)对于区间(1,2)中的任意常数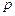 ,是否存在
,是否存在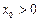 使
使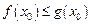 成立?
成立?若存在,求出符合条件的一个
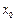 ;否则,说明理由.
;否则,说明理由.(Ⅰ)略 (Ⅱ) 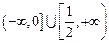 (Ⅲ)不存在
(Ⅲ)不存在
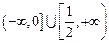 (Ⅲ)不存在
(Ⅲ)不存在:(Ⅰ)证明:当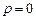 时,
时,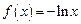 .令
.令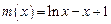 ,则
,则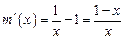 .
.
若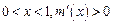 ,
,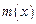 递增;若
递增;若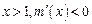 ,
,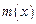 递减,
递减,
则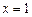 是
是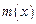 的极(最)大值点.于是
的极(最)大值点.于是
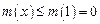 ,即
,即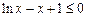 .故当
.故当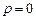 时,有
时,有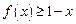 .
.
(Ⅱ)解:对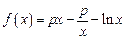 求导,得
求导,得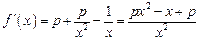 .
.
①若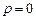 ,
,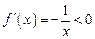 ,则
,则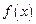 在
在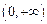 上单调递减,故
上单调递减,故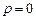 合题意.
合题意.
②若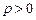 ,
,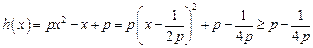 .
.
则必须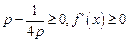 ,故当
,故当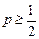 时,
时,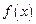 在
在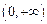 上单调递增.
上单调递增.
③若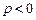 ,
,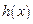 的对称轴
的对称轴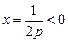 ,则必须
,则必须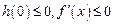 ,
,
故当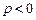 时,
时,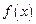 在
在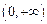 上单调递减.
上单调递减.
综合上述,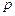 的取值范围是
的取值范围是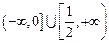 .
.
(Ⅲ)解:令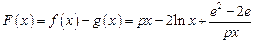 .则问题等价于
.则问题等价于
找一个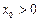 使
使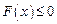 成立,故只需满足函数的最小值
成立,故只需满足函数的最小值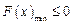 即可.
即可.
因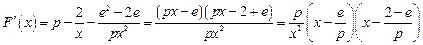 ,
,
而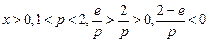 ,
,
故当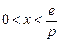 时,
时,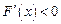 ,
,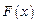 递减;当
递减;当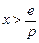 时,
时,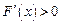 ,
,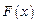 递增.
递增.
于是,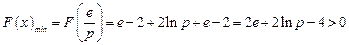 .与上述要求
.与上述要求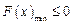 相矛盾,故不存在符合条件的
相矛盾,故不存在符合条件的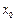 .
.
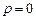 时,
时,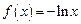 .令
.令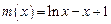 ,则
,则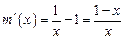 .
.若
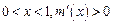 ,
,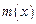 递增;若
递增;若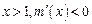 ,
,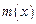 递减,
递减,则
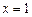 是
是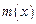 的极(最)大值点.于是
的极(最)大值点.于是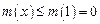 ,即
,即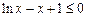 .故当
.故当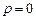 时,有
时,有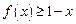 .
.(Ⅱ)解:对
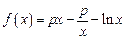 求导,得
求导,得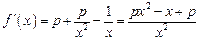 .
.①若
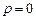 ,
,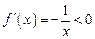 ,则
,则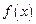 在
在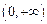 上单调递减,故
上单调递减,故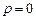 合题意.
合题意.②若
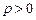 ,
,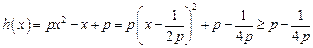 .
.则必须
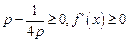 ,故当
,故当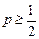 时,
时,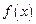 在
在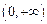 上单调递增.
上单调递增.③若
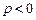 ,
,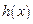 的对称轴
的对称轴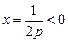 ,则必须
,则必须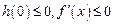 ,
,故当
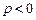 时,
时,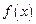 在
在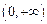 上单调递减.
上单调递减.综合上述,
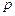 的取值范围是
的取值范围是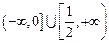 .
.(Ⅲ)解:令
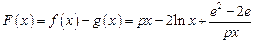 .则问题等价于
.则问题等价于找一个
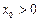 使
使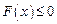 成立,故只需满足函数的最小值
成立,故只需满足函数的最小值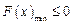 即可.
即可.因
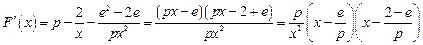 ,
,而
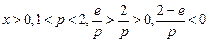 ,
,故当
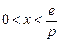 时,
时,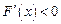 ,
,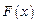 递减;当
递减;当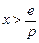 时,
时,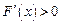 ,
,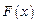 递增.
递增.于是,
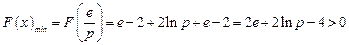 .与上述要求
.与上述要求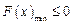 相矛盾,故不存在符合条件的
相矛盾,故不存在符合条件的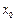 .
.
练习册系列答案
相关题目
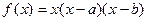 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))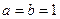 ,求函数
,求函数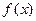 的单调递增区间;
的单调递增区间; 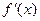 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|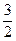 恒成立,求函数
恒成立,求函数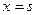 和
和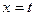 处取得极值,且
处取得极值,且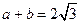 ,证明:
,证明: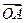 与
与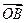 不可能垂直.
不可能垂直.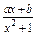 ,b为常数.
,b为常数.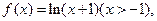 设
设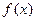 的反函数为
的反函数为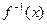 。
。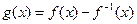 的单调区间;(II)若对任意
的单调区间;(II)若对任意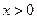 ,不等式
,不等式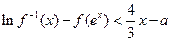 恒成立,求实数
恒成立,求实数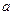 的取值范围。
的取值范围。
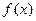 是二次函数,不等式
是二次函数,不等式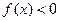 的解集是
的解集是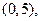 且
且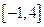 上的最大值是12。
上的最大值是12。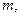 使得方程
使得方程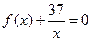 在区间
在区间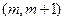 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出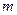 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。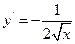 ,则
,则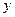 的表达式为( )
的表达式为( )