题目内容
7.已知点P(sinα-cosα,tanα)在第一象限,在[0,2π]内求α的取值范围.分析 由题意可知sinα-cosα>0,且tanα>0,得到sinα>cosα,且sinαcosα>0,由此可得α的范围.
解答 解:∵点P(sinα-cosα,tanα)在第一象限,
∴sinα-cosα>0,且tanα>0,
即sinα>cosα,且sinαcosα>0,
∴$\frac{π}{4}$<α<$\frac{π}{2}$或π<α<$\frac{5π}{4}$.
点评 本题考查三角函数值的符号,考查数学转化思想方法,是基础题.

练习册系列答案
相关题目
2.$\int_{-\frac{{\sqrt{3}}}{2}}^{\frac{{\sqrt{3}}}{2}}{\sqrt{1-{x^2}}dx}$=$\frac{3\sqrt{3}+4π}{12}$.
16.设a=e${\;}^{\frac{1}{2}}$,b=ln$\frac{1}{2}$,c=log2$\sqrt{2}$,则( )
| A. | a>c>b | B. | b>a>c | C. | c>b>a | D. | a>b>c |
14.从一块短轴成为2m的椭圆形板材中截取一块面积最大的矩形,若椭圆的离心率为e,且e∈[$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{21}}{5}$],则该矩形面积的取值范围是( )
| A. | [m2,2m2] | B. | [2m2,3m2] | C. | [3m2,4m2] | D. | [4m2,5m2] |
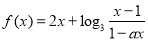 为奇函数,
为奇函数,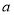 为常数.
为常数.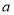 的值;
的值;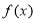 的单调区间;
的单调区间;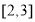 上的每一个
上的每一个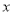 值,不等式
值,不等式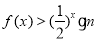 恒成立,求实数
恒成立,求实数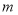 的取值范围.
的取值范围.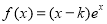 (
(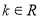 ).
). 的单调区间和极值;
的单调区间和极值;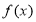 在
在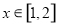 上的最小值.
上的最小值. ,若对
,若对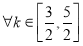 及
及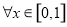 有
有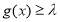 恒成立,求实数
恒成立,求实数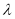 的取值范围.
的取值范围. ,
, (
( ),且
),且 ,点
,点 在圆
在圆 上,则
上,则 ( )
( ) B.
B.
 D.
D.