题目内容
16.设a=e${\;}^{\frac{1}{2}}$,b=ln$\frac{1}{2}$,c=log2$\sqrt{2}$,则( )| A. | a>c>b | B. | b>a>c | C. | c>b>a | D. | a>b>c |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:a=e${\;}^{\frac{1}{2}}$>1,b=ln$\frac{1}{2}$<0,c=log2$\sqrt{2}$=$\frac{1}{2}$,
∴a>c>b.
故选:A.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知F是双曲线C:y2-mx2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
2.若直线y=x+b与圆x2+y2=1有公共点,则实数b的取值范围是( )
| A. | [-1,1] | B. | [0,1] | C. | [0,$\sqrt{2}$] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
3.已知函数f(x)=$\frac{lnx}{x}$,关于x的不等式f2(x)-af(x)>0有且只有三个整数解,则实数a的取值范围是( )
| A. | [$\frac{ln5}{5}$,$\frac{ln2}{2}$) | B. | [$\frac{ln5}{5}$,$\frac{ln3}{3}$) | C. | ($\frac{ln5}{5}$,$\frac{ln2}{2}$] | D. | ($\frac{ln5}{5}$,$\frac{ln3}{3}$] |
 和
和 是方程
是方程 的两根,则
的两根,则 之间的关系是( )
之间的关系是( ) B.
B.
 D.
D.
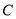 :
: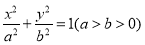 的左焦点为
的左焦点为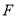 ,
, 为椭圆上一点,
为椭圆上一点,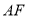 交
交 轴于点
轴于点 ,且
,且 为
为 的中点.
的中点. 的方程;
的方程;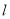 与椭圆
与椭圆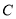 有且只有一个公共点
有且只有一个公共点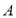 ,平行于
,平行于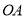 的直线交
的直线交 于
于 ,交椭圆
,交椭圆 于不同的亮点
于不同的亮点 ,
, ,问是否存在常熟
,问是否存在常熟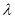 ,使得
,使得 ,若存在,求出
,若存在,求出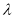 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.