题目内容
已知函数![]() ,
,![]() 其中e为自然对数的底数,a
其中e为自然对数的底数,a![]()
(I)设a=-1 ,x![]() [-1,1],求函数y=f(x)的极值;
[-1,1],求函数y=f(x)的极值;
(Ⅱ)若对于任意的a>0,都有f(x)![]() 成立,求x的取值范围。
成立,求x的取值范围。
解:(Ⅰ)当![]() 时,
时,![]() ,
,![]() .
.
当![]() 在
在![]() 上变化时,
上变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| - |
| + | ||
|
|
|
|
|
|
|
∴![]() 时,
时,![]() ,
,![]() .
.
(Ⅱ)∵![]() ,
,![]() ,
,
∴原不等式等价于:![]() ,
,
即![]() , 亦即
, 亦即![]() .
.
∴对于任意的![]() ,原不等式恒成立,等价于
,原不等式恒成立,等价于![]() 对
对![]() 恒成立,
恒成立,
∵对于任意的![]() 时,
时, ![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
∴只需![]() ,即
,即![]() ,解之得
,解之得![]() 或
或![]() .
.
因此,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
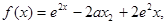 其中e为自然对数的底数。
其中e为自然对数的底数。 其中e为自然对数的底数,a,b,c为常数,若函数
其中e为自然对数的底数,a,b,c为常数,若函数 且
且
 在区间[1,2]上是增函数,求实数a的取值范围。
在区间[1,2]上是增函数,求实数a的取值范围。