题目内容
已知函数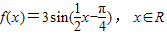 .
.(1)画出函数f(x)在长度为一个周期的闭区间上的简图.
(2)设函数g(x)=|f(x)|,求g(x)的周期、单调递减区间.
【答案】分析:(1)利用描点法画函数图象,第一步列表,令函数解析式中的角分别为0, ,π,
,π, ,2π,求出x的值,且代入函数解析式求出对应的函数值y的值,找出函数图象上五点坐标,在平面直角坐标系中描出五个点,用平滑的曲线画出函数图象即可;
,2π,求出x的值,且代入函数解析式求出对应的函数值y的值,找出函数图象上五点坐标,在平面直角坐标系中描出五个点,用平滑的曲线画出函数图象即可;
(2)找出函数f(x)解析式中ω的值,代入周期公式T= ,求出函数f(x)的周期T,然后利用T′=
,求出函数f(x)的周期T,然后利用T′= 即可求出g(x)的周期,根据正弦函数的图象与性质得出g(x)的单调递减区间为[kπ+
即可求出g(x)的周期,根据正弦函数的图象与性质得出g(x)的单调递减区间为[kπ+ ,kπ+π],列出关于x的不等式,求出不等式的解集即可得到函数g(x)的单调递减区间.
,kπ+π],列出关于x的不等式,求出不等式的解集即可得到函数g(x)的单调递减区间.
解答:解:(1)根据题意列出表格得:

(2)∵ω= ,
,
∴函数f(x)的周期T= =4π,
=4π,
∴g(x)的周期 ,
,
令 ,
,
解得: ,
,
∴函数g(x)的单调递减区间为 .
.
点评:此题考查了三角函数的周期性及其求法,正弦函数的图象与性质,正弦函数的单调性,以及利用五点法作三角函数的图象,熟练掌握正弦函数的图象与性质是解本题的关键.
 ,π,
,π, ,2π,求出x的值,且代入函数解析式求出对应的函数值y的值,找出函数图象上五点坐标,在平面直角坐标系中描出五个点,用平滑的曲线画出函数图象即可;
,2π,求出x的值,且代入函数解析式求出对应的函数值y的值,找出函数图象上五点坐标,在平面直角坐标系中描出五个点,用平滑的曲线画出函数图象即可;(2)找出函数f(x)解析式中ω的值,代入周期公式T=
 ,求出函数f(x)的周期T,然后利用T′=
,求出函数f(x)的周期T,然后利用T′= 即可求出g(x)的周期,根据正弦函数的图象与性质得出g(x)的单调递减区间为[kπ+
即可求出g(x)的周期,根据正弦函数的图象与性质得出g(x)的单调递减区间为[kπ+ ,kπ+π],列出关于x的不等式,求出不等式的解集即可得到函数g(x)的单调递减区间.
,kπ+π],列出关于x的不等式,求出不等式的解集即可得到函数g(x)的单调递减区间.解答:解:(1)根据题意列出表格得:
| x |  |  |  |  |  |
 |  | π |  | 2π | |
3sin( ) ) | 3 | -3 |

(2)∵ω=
 ,
,∴函数f(x)的周期T=
 =4π,
=4π,∴g(x)的周期
 ,
,令
 ,
,解得:
 ,
,∴函数g(x)的单调递减区间为
 .
.点评:此题考查了三角函数的周期性及其求法,正弦函数的图象与性质,正弦函数的单调性,以及利用五点法作三角函数的图象,熟练掌握正弦函数的图象与性质是解本题的关键.

练习册系列答案
相关题目
 .
. 的图象,写出函数
的图象,写出函数 的不等式
的不等式
 .
. (
(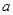 ∈R).
∈R). 的图象;
的图象;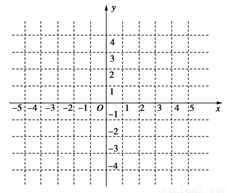
 ,
, 图像;
图像; 的值;
的值; 时,求
时,求
 ,
, 图像;
图像; 的值;
的值; 时,求
时,求