题目内容
（本小题满分12分）已知函数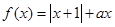
(
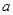∈R).
（1）画出当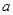=2时的函数
的图象；
（2）若函数在R上具有单调性，求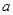的取值范围.
【答案】
（1）
；（2）
。
【解析】本试题主要是考查了分段函数的图像以及函数单调性的运用。
（1）先分析当
时
，然后利用描点连线，作图。
（2）因为函数
在R上具有单调性，则每段都有单调性，且在分段点处函数值满足不等式关系，得到结论。
（1）当时
图象如右图所示
（2）由已知可得
①当函数在R上单调递增时，
由
可得
②当函数在R上单调递减时，
由
可得
综上可知，
的取值范围是
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
