题目内容
已知函数 .
.
(1)画出函数 的图象,写出函数
的图象,写出函数 的单调区间;
的单调区间;
(2)解关于 的不等式
的不等式
 .
.
【答案】
(1) 单调递减区间是 ,单调递增区间是
,单调递增区间是 .
.
(2) 当 时,
时, 恒成立,即不等式的解为
恒成立,即不等式的解为 ;
;
当 时,不等式的解为
时,不等式的解为 ;
;
当 时,不等式的解为
时,不等式的解为 .
.
【解析】
试题分析:解析: .
.
画出函数 的图象如图中的折线,其单调递减区间是
的图象如图中的折线,其单调递减区间是 ,单调递增区间是
,单调递增区间是 .
.
(2)结合图象可知:
当 时,
时, 恒成立,即不等式的解为
恒成立,即不等式的解为 ;
;
当 时,不等式的解为
时,不等式的解为 ;
;
当 时,不等式的解为
时,不等式的解为 .
.
考点:绝对值函数
点评:利用去掉绝对值符号来得到函数解析式,结合函数性质来得到不等式的解集,属于基础题。

练习册系列答案
相关题目
 ,
, 图像;
图像; 的值;
的值; 时,求
时,求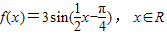 .
. ,
, 图像;
图像; 的值;
的值; 时,求
时,求
 ,
, 图像;
图像; 的值;
的值; 时,求
时,求