题目内容
【题目】某种体育比赛的规则是：进攻队员与防守队员均在安全线
的垂线
上（
为垂足），且分别位于距为
和
的点
和点
处，进攻队员沿直线
向安全线跑动，防守队员沿直线方向拦截，设和
交于点
，若在点，防守队员比进攻队员先到或同时到，则进攻队员失败，已知进攻队员速度是防守队员速度的两倍，且他们双方速度不变，问进攻队员的路线应为什么方向才能取胜？
【答案】进攻队员的路线
与
所成角大于30°即可
【解析】
由题意建立平面直角坐标系，求出点M的轨迹方程，利用数形结合法求得进攻队员获胜的路线是什么．
如图，以
为
轴，
为原点建立直角坐标系，
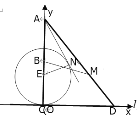
设防守队员速度为
，则进攻队员速度为
，
设点
坐标为
，进攻队员与防守队员跑到点所需时间分别为
，
，
若
，则
即
整理得
这说明点应在圆
：
以外，进攻队员方能取胜.
设
为圆的切线，
为切点，
在
中，
，
,
所以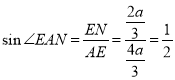
，
故
所以进攻队员的路线与所成角大于30°即可.
练习册系列答案
考前必练系列答案
相关题目
